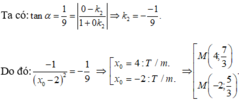Các câu hỏi tương tự
Cho hàm số
y
x
+
2
2
x
+
3
1
. Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ 0. A: x + y 0 B: x + y + 2 0 C: x + y – 2 0 D: Cả A và C đúng
Đọc tiếp
Cho hàm số y = x + 2 2 x + 3 1 . Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ 0.
A: x + y = 0
B: x + y + 2 = 0
C: x + y – 2 = 0
D: Cả A và C đúng
Cho hàm số y = x3 – 3x2 + 1 (C). Tìm tổng hoành độ của hai điểm A; B trên đồ thị hàm số sao cho tiếp tuyến của đồ thị (C) tại A; B song song với nhau và A B = 4 2
A: 1
B: 2
C: 3
D: 5
Cho hàm số y=\(x^3-3x^2-1\)có đồ thị (C).Điểm M(a;b) trên(C) có hoành độ thuộc [2;3] sao cho tiếp tuyến của (C) tại M có hệ số góc lớn nhất.Khi đó, S=a+b=?
a) tìm hệ số góc của tiếp tuyến của đồ thị hàm số y=-x^3+3x-2 (c) tại điểm có hoành độ -3
b) viết phương trình tiếp tuyến của đồ thị hàm số (c) trên tại điểm ( ứng với tiếp điểm ) có hoành độ -3
Cho hàm số
y
3
x
+
1
x
+
1
1
. Diện tích của tam giác tạo bởi các trục tọa độ và tiếp tuyến của đồ thị của hàm số (1) tại điểm M(-2; 5) là a/b ( phân số tối giản) .Tính a + b. A: 81 B: 4 C: 85 D: đáp án khác
Đọc tiếp
Cho hàm số y = 3 x + 1 x + 1 1 . Diện tích của tam giác tạo bởi các trục tọa độ và tiếp tuyến của đồ thị của hàm số (1) tại điểm M(-2; 5) là a/b ( phân số tối giản) .Tính a + b.
A: 81
B: 4
C: 85
D: đáp án khác
Cho hàm số y = x 3 - 3 x + 1 có đồ thị là (C).Giả sử (d) là tiếp tuyến của (C) tại điểm có hoành độ x = 2, đồng thời (d) cắt đồ thị (C) tại N, tìm tọa độ N.
A. N(1;-1)
B. N(2;3)
C. N(-4;-51)
D. N(3;19)
Cho hàm số y=f(x)=-x3+x2-1 có đồ thị (C):
Viết phương trình tiếp tuyến với đồ thị của hàm số tại điểm có hoành độ bằng 2
cho hàm số y=x^3+3x^2+1 có đồ thị (C)/.Gọi d là tiếp tuyến của C tại điểm A(1,5) và B la giao điểm thứ hai của d với C khi đó diện tích tam giác oab bằng
Cho hàm số
y
cos
2
x
.a) Chứng minh rằng cos
2
x
+
k
π
cos
2
x
với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số
y
cos
2
x
.b) Viết phương...
Đọc tiếp
Cho hàm số y = cos 2 x .
a) Chứng minh rằng cos 2 x + k π = cos 2 x với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số y = cos 2 x .
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π / 3 .
c) Tìm tập xác định của hàm số : z = 1 - cos 2 x 1 + cos 2 2 x