Các câu hỏi tương tự
Biết hàm số f(x) xác định trên R và có đạo hàm f’(x) (x – 1)x2(x + 1)3(x + 2)4. Hỏi hàm số có bao nhiêu điểm cực trị? A. 4. B. 1 C. 2 D. 3
Đọc tiếp
Biết hàm số f(x) xác định trên R và có đạo hàm f’(x) = (x – 1)x2(x + 1)3(x + 2)4. Hỏi hàm số có bao nhiêu điểm cực trị?
A. 4.
B. 1
C. 2
D. 3
Cho hàm số y = f ( x ) có đạo hàm trên R là f ' ( x ) = ( 2 x + 1 ) ( x - 3 ) ( x + 5 ) 4 . Hỏi hàm số đã cho có tất cả bao nhiêu điểm cực trị
A. 2
B. 1
C. 4
D. 3
Cho hàm số liên tục trên khoảng (a;b) và
x
0
∈
(
a
;
b
)
.
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?(1) Hàm số đạt cực trị tại điểm
x
0
khi và chỉ khi
f
(
x
0
)
0
.
(2) Nếu hàm số
y
f
(
x
)
có đạo hàm và có đạo...
Đọc tiếp
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ ( a ; b ) . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' ( x 0 ) = 0 .
(2) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = f ' ' ( x 0 ) = 0 thì điểm x 0 không phải là điểm cực trị của hàm số y = f ( x ) .
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
(4) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = 0 , f ' ' ( x 0 ) > 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
A. 1
B. 2
C. 0
D. 3
chỉ mik cách lập nhóm nhaTrích một số bài toán trong đề:+ Trên mặt phẳng phức, tập hợp điểm biểu diễn cho số phức z thỏa mãn điều kiện /z/ 2 là:A. Đường tròn tâm O, bán kính R 2B. Đường tròn tâm O, bán kính R 4C. Đường tròn tâm O, bán kính R 1/2D. Đường tròn tâm O , bán kính R căn 2+ Cho hàm số y f(x) xác định, liên tục trên R và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây đúng?A. Hàm số y f(x) có giá trị cực đại bằng 0B. Giá trị lớn nhất của hàm số y f(x) trên tập R là 1C. Hà...
Đọc tiếp
chỉ mik cách lập nhóm nha
Trích một số bài toán trong đề:
+ Trên mặt phẳng phức, tập hợp điểm biểu diễn cho số phức z thỏa mãn điều kiện /z/ = 2 là:
A. Đường tròn tâm O, bán kính R = 2
B. Đường tròn tâm O, bán kính R = 4
C. Đường tròn tâm O, bán kính R = 1/2
D. Đường tròn tâm O , bán kính R = căn 2
+ Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây đúng?
A. Hàm số y = f(x) có giá trị cực đại bằng 0
B. Giá trị lớn nhất của hàm số y = f(x) trên tập R là 1
C. Hàm số y = f(x) đạt cực đại tại x = 0 và cực tiểu tại x = -1
D. Hàm số y = f(x) có đúng một cực trị
+ Tìm phần thực của số phức (2 + 3i).i^10
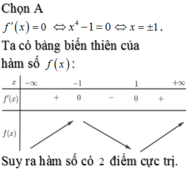
Cho hàm số y f(x) xác định trên R và có đồ thị của hàm số y f’(x) như hình vẽ. Hàm số y f(x) + 4x có bao nhiêu điểm cực trị? A. 1. B. 2. C. 3. D. 4.
Đọc tiếp
Cho hàm số y= f(x) xác định trên R và có đồ thị của hàm số y= f’(x) như hình vẽ.
Hàm số y= f(x) + 4x có bao nhiêu điểm cực trị?
A. 1.
B. 2.
C. 3.
D. 4.
Cho hàm số y = f ( x ) có đạo hàm trên R là f ' ( x ) = ( x - 2018 ) ( x - 2019 ) ( x - 2020 ) 4 . Hàm số đã cho có bao nhiêu điểm cực trị?
A. 2
B. 1
C. 4
D. 3
Xét các khẳng định sau: (1) Nếu hàm số yf(x) xác định trên R thỏa mãn f(-1).f(0)0 thì đồ thị của hàm số yf(x) và trục hoành có ít nhất 1 điểm chung. (2) Nếu hàm số yf(x) xác định trên R thỏa mãn f(-1).f(0)0 và f(0).f(1)0 thì đồ thị của hàm số yf(x) và trục hoành có ít nhất 2 điểm chung. Phát biểu nào sau đây đúng? A. Khẳng định đúng và khẳng định sai. B. Khẳng định sai và khẳng định đúng. C. Khẳng định sai và khẳng định sai. D. Khẳng định đúng và khẳng định đúng.
Đọc tiếp
Xét các khẳng định sau:
(1) Nếu hàm số y=f(x) xác định trên R thỏa mãn f(-1).f(0)<0 thì đồ thị của hàm số y=f(x) và trục hoành có ít nhất 1 điểm chung.
(2) Nếu hàm số y=f(x) xác định trên R thỏa mãn f(-1).f(0)<0 và f(0).f(1)<0 thì đồ thị của hàm số y=f(x) và trục hoành có ít nhất 2 điểm chung.
Phát biểu nào sau đây đúng?
A. Khẳng định ![]() đúng và khẳng định
đúng và khẳng định ![]() sai.
sai.
B. Khẳng định ![]() sai và khẳng định
sai và khẳng định ![]() đúng.
đúng.
C. Khẳng định ![]() sai và khẳng định
sai và khẳng định ![]() sai.
sai.
D. Khẳng định ![]() đúng và khẳng định
đúng và khẳng định ![]() đúng.
đúng.
Cho hàm số yf(x) xác định trên
ℝ
1
, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽHàm số
y
f
(
x
)
có bao nhiêu điểm cực trị? A. 4. B. 3. C. 2. D. 5.
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ \ 1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ
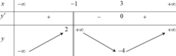
Hàm số y = f ( x ) có bao nhiêu điểm cực trị?
A. 4.
B. 3.
C. 2.
D. 5.
Cho f(x) là hàm số bậc 4 thỏa mãn fleft(0right)dfrac{-1}{ln2}. Hàm số fleft(xright) có bảng biến thiên như sau: Hàm số gleft(xright)left|fleft(-x^2right)-x^2+dfrac{2^{x^2}}{ln2}right| có bao nhiêu điểm cực trị?A. 3B.2C.4D.5
Đọc tiếp
Cho f(x) là hàm số bậc 4 thỏa mãn \(f\left(0\right)=\dfrac{-1}{\ln2}\). Hàm số \(f'\left(x\right)\) có bảng biến thiên như sau:
Hàm số \(g\left(x\right)=\left|f\left(-x^2\right)-x^2+\dfrac{2^{x^2}}{\ln2}\right|\) có bao nhiêu điểm cực trị?
A. 3
B.2
C.4
D.5