Các câu hỏi tương tự
Cho hàm số yf(x) có đạo hàm liên tục trên
−
1
;
2
. Đồ thị của hàm số yf(x) được cho như hình vẽ. Diện tích các hình phẳng (K), (H) lần lượt là
5
12
và
8
3
.
Biết
f
−
1
19
12...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên − 1 ; 2 . Đồ thị của hàm số y=f'(x) được cho như hình vẽ. Diện tích các hình phẳng (K), (H) lần lượt là 5 12 và 8 3 . Biết f − 1 = 19 12 , tính f(2).
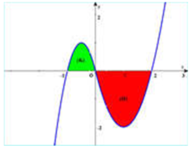
A. f 2 = 23 6 .
B. f 2 = − 2 3 .
C. f 2 = 2 3 .
D. f 2 = 11 6 .
Cho hàm số y f(x) có đạo hàm liên tục trên [-1;2]. Đồ thị của hàm số y f(x) được cho như hình bên. Diện tích các hình phẳng (K), (H) lần lượt là
5
12
và
8
3
. Biết
f
-
1
19
12
, tính f(2) A.
f
2
-
2
3...
Đọc tiếp
Cho hàm số y =f(x) có đạo hàm liên tục trên [-1;2]. Đồ thị của hàm số y = f'(x) được cho như hình bên. Diện tích các hình phẳng (K), (H) lần lượt là 5 12 và 8 3 . Biết f - 1 = 19 12 , tính f(2)
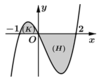
A. f 2 = - 2 3
B. f 2 = 2 3
C. f 2 = 11 6
D. f 2 = 3
Cho hàm số f(x), g(x) có đồ thị như hình vẽ. Đặt
h
x
f
x
g
x
. Tính h (2) đạo hàm của hàm số h(x) tại x 2. A.
h
2
4
49
B.
h
2
-
4...
Đọc tiếp
Cho hàm số f(x), g(x) có đồ thị như hình vẽ. Đặt h x = f x g x . Tính h' (2) đạo hàm của hàm số h(x) tại x = 2.
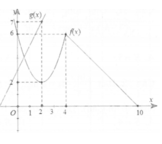
A. h ' 2 = 4 49
B. h ' 2 = - 4 49
C. h ' 2 = 2 7
D. h ' 2 = - 2 7
Cho hàm số
y
f
(
x
)
có đạo hàm trên
ℝ
. Xét các hàm số
g
(
x
)
f
x
−
f
2
x
và
h
(
x
)
f
(
x
)
−
f
(
4
x
)
. Biết rằng
g...
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm trên ℝ . Xét các hàm số g ( x ) = f x − f 2 x và h ( x ) = f ( x ) − f ( 4 x ) . Biết rằng g ' ( 1 ) = 18 và g ' ( 2 ) = 1000 . Tính h ' ( 1 ) :
A. − 2018
.
B. 2018
C. 2020
D. − 2020
Cho hàm số f(x) liên tục trên R và có
∫
0
1
f
(
x
)
d
x
2
;
∫
0
3
f
(
x
)
d
x
6
.
T
í
n
h
I
∫
-
1
1...
Đọc tiếp
Cho hàm số f(x) liên tục trên R và có ∫ 0 1 f ( x ) d x = 2 ; ∫ 0 3 f ( x ) d x = 6 . T í n h I = ∫ - 1 1 f ( | 2 x - 1 | ) dx
A. I= 2/3
B. I= 4
C. I= 3/2
D. I= 6
Cho hàm số f(x) thỏa mãn
f
x
2
+
f
x
.
f
x
2018
x
∀
x
∈
R
và f(0) f’(0) 1. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x 0; x 2. Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục...
Đọc tiếp
Cho hàm số f(x) thỏa mãn f ' x 2 + f x . f " x = 2018 x ∀ x ∈ R và f(0) = f’(0) = 1. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x = 0; x = 2. Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục Ox.
A. V = 8090 3 2
B. V = 4036π
C. V = 8090 3 π
D. V = 8090π/3
Cho hàm số f(x) thỏa mãn
f
x
2
+
f
x
f
x
2018
x
,
∀
x
∈
ℝ
và
f
0
f
0
1
. Gọi (H) là hình phẳng giới hạn bởi đồ th...
Đọc tiếp
Cho hàm số f(x) thỏa mãn f ' x 2 + f x f ' ' x = 2018 x , ∀ x ∈ ℝ và f 0 = f ' 0 = 1 . Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x = 0 , x = 2 . Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục Ox.
A. V = 8090 3 2 π
B. V = 4036 π
C. V = 8090 3 π
D. V = 8090 3 π
Cho F(x) là một nguyên hàm của hàm số f(x) trên đoạn [1;3], F(1)3,F(3)5 và
∫
1
3
(
x
4
-
8
x
)
f
(
x
)
dx
12
.
Tính
I
∫
1
3
(
x
3
-
2
)
F
(
x...
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số f(x) trên đoạn [1;3], F(1)=3,F(3)=5 và ∫ 1 3 ( x 4 - 8 x ) f ( x ) dx = 12 . Tính I = ∫ 1 3 ( x 3 - 2 ) F ( x ) dx .
A. I= 147 2
B. I= 147 3
C. I= - 147 2
D. I= 147.
Cho hàm số f(x) liên tục trên
ℝ
và
∫
0
1
f
(
x
)
d
x
2
;
∫
0
3
f
x
d
x
6
. Tính
I
∫
-
1
1
f
2...
Đọc tiếp
Cho hàm số f(x) liên tục trên ℝ và ∫ 0 1 f ( x ) d x = 2 ; ∫ 0 3 f x d x = 6 . Tính I = ∫ - 1 1 f 2 x - 1 d x ?
A. I = 2 3
B. I = 4
C. I = 3 2
D. I = 6
Cho hàm số y f (x) có đạo hàm trên R. Xét tính đúng sai của các mệnh đề sau.(I): Nếu f’(x) 0 trên khoảng (x0–h;x0) và f’(x) 0 trên khoảng (x0;x0+h) (h0) thì hàm số đạt cực đại tại điểm x0 (II): Nếu hàm số đạt cực đại tại điểm x0 thì tồn tại các khoảng (x0–h;x0), (x0;x0+h) (h0) sao cho f’(x) 0 trên khoảng (x0–h;x0) và f’(x) 0 trên khoảng (x0;x0+h) A. Cả (I) và (II) cùng sai B. Mệnh đề (I) đúng, mệnh đề (II) sai C. Mệnh đề (I) sai, mệnh đề (II) đúng D. Cả (I) và (II) cùng đúng
Đọc tiếp
Cho hàm số y = f (x) có đạo hàm trên R. Xét tính đúng sai của các mệnh đề sau.
(I): Nếu f’(x) > 0 trên khoảng (x0–h;x0) và f’(x) < 0 trên khoảng (x0;x0+h) (h>0) thì hàm số đạt cực đại tại điểm x0
(II): Nếu hàm số đạt cực đại tại điểm x0 thì tồn tại các khoảng (x0–h;x0), (x0;x0+h) (h>0) sao cho f’(x) > 0 trên khoảng (x0–h;x0) và f’(x) < 0 trên khoảng (x0;x0+h)
A. Cả (I) và (II) cùng sai
B. Mệnh đề (I) đúng, mệnh đề (II) sai
C. Mệnh đề (I) sai, mệnh đề (II) đúng
D. Cả (I) và (II) cùng đúng