Các câu hỏi tương tự
Cho hàm số yf(x) có đạo hàm liên tục trên
−
1
;
2
. Đồ thị của hàm số yf(x) được cho như hình vẽ. Diện tích các hình phẳng (K), (H) lần lượt là
5
12
và
8
3
.
Biết
f
−
1
19
12...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên − 1 ; 2 . Đồ thị của hàm số y=f'(x) được cho như hình vẽ. Diện tích các hình phẳng (K), (H) lần lượt là 5 12 và 8 3 . Biết f − 1 = 19 12 , tính f(2).
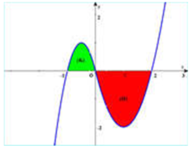
A. f 2 = 23 6 .
B. f 2 = − 2 3 .
C. f 2 = 2 3 .
D. f 2 = 11 6 .
Cho hàm số y f(x) có đạo hàm liên tục trên [-1;2]. Đồ thị của hàm số y f(x) được cho như hình bên. Diện tích các hình phẳng (K), (H) lần lượt là
5
12
và
8
3
. Biết
f
-
1
19
12
, tính f(2) A.
f
2
-
2
3...
Đọc tiếp
Cho hàm số y =f(x) có đạo hàm liên tục trên [-1;2]. Đồ thị của hàm số y = f'(x) được cho như hình bên. Diện tích các hình phẳng (K), (H) lần lượt là 5 12 và 8 3 . Biết f - 1 = 19 12 , tính f(2)
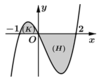
A. f 2 = - 2 3
B. f 2 = 2 3
C. f 2 = 11 6
D. f 2 = 3
Cho hàm số
y
f
(
x
)
có đạo hàm trên
ℝ
. Xét các hàm số
g
(
x
)
f
x
−
f
2
x
và
h
(
x
)
f
(
x
)
−
f
(
4
x
)
. Biết rằng
g...
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm trên ℝ . Xét các hàm số g ( x ) = f x − f 2 x và h ( x ) = f ( x ) − f ( 4 x ) . Biết rằng g ' ( 1 ) = 18 và g ' ( 2 ) = 1000 . Tính h ' ( 1 ) :
A. − 2018
.
B. 2018
C. 2020
D. − 2020
Cho F(x) là một nguyên hàm của hàm số f(x) trên đoạn [1;3], F(1)3,F(3)5 và
∫
1
3
(
x
4
-
8
x
)
f
(
x
)
dx
12
.
Tính
I
∫
1
3
(
x
3
-
2
)
F
(
x...
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số f(x) trên đoạn [1;3], F(1)=3,F(3)=5 và ∫ 1 3 ( x 4 - 8 x ) f ( x ) dx = 12 . Tính I = ∫ 1 3 ( x 3 - 2 ) F ( x ) dx .
A. I= 147 2
B. I= 147 3
C. I= - 147 2
D. I= 147.
Cho hàm số y f(x) có bảng biến thiên như sau: (I): Tập xác định của f(x): R {1} (II): Hàm số f(x) có đúng 1 điểm cực trị (III): min f(x) -2 (IV): A(-1; 3) là điểm cực đại của đồ thị hàm số Trong các phát biểu trên, có bao nhiêu phát biểu đúng? A. 2 B. 3 C. 1 D. 0
Đọc tiếp
Cho hàm số y = f(x) có bảng biến thiên như sau:
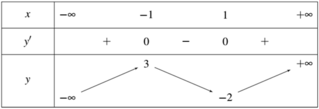
(I): Tập xác định của f(x): R \ {1}
(II): Hàm số f(x) có đúng 1 điểm cực trị
(III): min f(x) = -2
(IV): A(-1; 3) là điểm cực đại của đồ thị hàm số
Trong các phát biểu trên, có bao nhiêu phát biểu đúng?
A. 2
B. 3
C. 1
D. 0
Cho hàm số f(x) thỏa mãn
∫
1
2
(
2
x
+
3
)
f
(
x
)
d
x
15
và 7f(2)-5f(1)8. Tính
I
∫
1
2
f
(
x
)
d
x
A.
I
7
2
B.
I...
Đọc tiếp
Cho hàm số f(x) thỏa mãn ∫ 1 2 ( 2 x + 3 ) f ' ( x ) d x = 15 và 7f(2)-5f(1)=8. Tính I = ∫ 1 2 f ( x ) d x
A. I = 7 2
B. I = - 2 7
C. I = 2 7
D. I = - 7 2
Cho hàm số f(x) thỏa mãn
f
x
2
+
f
x
.
f
x
2018
x
∀
x
∈
R
và f(0) f’(0) 1. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x 0; x 2. Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục...
Đọc tiếp
Cho hàm số f(x) thỏa mãn f ' x 2 + f x . f " x = 2018 x ∀ x ∈ R và f(0) = f’(0) = 1. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x = 0; x = 2. Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục Ox.
A. V = 8090 3 2
B. V = 4036π
C. V = 8090 3 π
D. V = 8090π/3
Cho hàm số f(x) có đạo hàm f(x)
(
x
+
1
)
2
(
x
-
1
)
3
(
2
-
x
)
. Hỏi hàm số đồng biến trên khoảng nào dưới đây? A. (1;2) B. (-1;1) C.
(
-
∞
;
1
)
D.
(
2
;
+
∞
)
Đọc tiếp
Cho hàm số f(x) có đạo hàm f'(x) = ( x + 1 ) 2 ( x - 1 ) 3 ( 2 - x ) . Hỏi hàm số đồng biến trên khoảng nào dưới đây?
A. (1;2)
B. (-1;1)
C. ( - ∞ ; 1 )
D. ( 2 ; + ∞ )
Cho hàm số f (x) có đạo hàm
f
(
x
)
(
x
+
1
)
2
(
x
-
1
)
3
(
2
-
x
)
Hỏi hàm số đồng biến trên khoảng nào dưới đây A.
(
2
;
+
∞
)
B. ...
Đọc tiếp
Cho hàm số f (x) có đạo hàm f ' ' ( x ) = ( x + 1 ) 2 ( x - 1 ) 3 ( 2 - x ) Hỏi hàm số đồng biến trên khoảng nào dưới đây
A. ( 2 ; + ∞ )
B. ( 1 ; 2 )
C. ( - ∞ ; - 1 )
D. ( - 1 ; 1 )
Cho hàm số f(x) có đạo hàm f ’ ( x ) = x 2019 ( x - 1 ) 2 ( x + 1 ) 3 . Số điểm cực đại của hàm số f(x) là
A. 1
B. -1
C. 0
D. 3



