Ta có f ' x = - m 2 + m + 1 x + 1 2 > 0
Suy ra f(x) là hàm đồng biến trên [0;1]
Do đó f 0 ≤ f x ≤ f 1 hay
- m 2 + m ≤ f x ≤ 1 2 - m 2 + m + 1
Khi đó
m i n x ∈ 0 ; 1 f x = - m 2 + m = - 2 ⇔ m = - 1 m = 2
Đáp án A
Ta có f ' x = - m 2 + m + 1 x + 1 2 > 0
Suy ra f(x) là hàm đồng biến trên [0;1]
Do đó f 0 ≤ f x ≤ f 1 hay
- m 2 + m ≤ f x ≤ 1 2 - m 2 + m + 1
Khi đó
m i n x ∈ 0 ; 1 f x = - m 2 + m = - 2 ⇔ m = - 1 m = 2
Đáp án A
Cho hàm số y = f ( x ) = x - m 2 x + 4 với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1
A. m = 2
B. m = 0
C. m 6
D. m = 3
Cho hàm số f ( x ) = sin x - m sin x + 1 . Tìm giá trị của tham số m để giá trị lớn nhất của hàm số trên đoạn 0 ; 2 π 3 bằng -2?
A. m = 5
B. m = 5 m = 2
C. m = 2
D. m = 3
Số các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số y = x - m 2 + m x + 1 trên đoạn [0;1] bằng -2 là:
A. 2
B. 0
C. 3
D. 1
Cho hàm số f(x)=(2 x +m)/(√x+1) với m là tham số thực, m>1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là
A. 1
B. 3
C. 0
D. 2
Cho hàm số f (x) có đạo hàm cấp hai liên tục trên đoạn [0;1] thoả mãn f ' ( x ) 2 + f x f ' ' x ≥ 1 ∀ m ∈ 0 ; 1 và f 2 0 + f 0 . f ' 0 = 3 2 Giá trị nhỏ nhất của tích phân ∫ 0 1 f 2 x d x bằng
A. 5 2
B. 1 2
C. 11 6
D. 7 2
Cho hàm số y=f(x) liên tục, không âm trên R thỏa mãn f ( x ) . f ' ( x ) = 2 x f ( x ) 2 + 1 và f(0)=0. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y=f(x) trên đoạn [1;3] lần lượt là:
A. M=20;m=2
B. M = 4 11 ; m = 3
C. M = 20 ; m = 2
D. M = 3 11 ; m = 3
Cho hàm số y = f(x) có đồ thị f'(x) như hình vẽ. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g x = f x 2 + x - 1 + 480 m x 2 + x + 2 nghịch biến trên (0;1)?
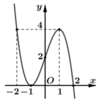
A. 4
B. 6
C. 7
D. 8
Cho hàm số f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tìm tất cả các giá trị thực của tham số m để hàm số y=f(|x|) có 5 cực trị
A. - 10 < m < 5 4
B. - 2 < m < 5
C. - 2 < m < 5 4
D. 5 4 < m < 2
Cho hàm số f ( x ) = x 3 - 3 x . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=|f(sinx+1)+2|. Giá trị biểu thức M + m bằng
A. 4.
B. 6.
C. 2.
D. 8.