Hàm số liên tục trên R trước hết hàm số liên tục tại x=1
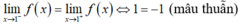
- Vậy không tồn tại a để hàm số liên tục trên R.
Hàm số liên tục trên R trước hết hàm số liên tục tại x=1
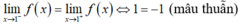
- Vậy không tồn tại a để hàm số liên tục trên R.
Cho hàm số . Tìm khẳng định đúng trong các khẳng định sau:
(I). f(x) liên tục tại x= 3
(II). f(x) gián đoạn tại x= 3 .
(III). f(x) liên tục trên R.
A. Chỉ (I) và (II).
B. Chỉ (II) và (III).
C. Chỉ (I) và (III).
D. Cả (I), (II), (III) đều đúng.
Tìm khẳng định đúng trong các khẳng định sau:
( I ) f ( x ) = x 5 - x 2 + 1 liên tục trên R
( II ) f ( x ) = 1 x 2 - 1 liên tục trên khoảng (-1; 1).
( III ) f ( x ) = x - 2 liên tục trên đoạn [2; +∞).
A. Chỉ (I) đúng.
B. Chỉ (I) và (II).
C. Chỉ (II) và (III).
D. Chỉ (I) và (III).
Cho hàm số f ( x ) = a 2 x 2 , x ≤ 2 , a ∈ ℝ ( 2 - a ) x 2 , x > 2 . Giá trị của a để f(x) liên tục trên R là:
A. 1 và 2
B. 1 và -1
C. -1 và 2.
D. 1 và -2
Cho hàm số f(x) xác định trên khoảng K chứa A. Hàm số f(x) liên tục tại x=a nếu:
A. lim x → a + f x = lim x → a - f x = a
B. f x có giới hạn khi x → a
C. lim x → a + f x = lim x → a - f x = + ∞
D. lim x → a f x = f a
Cho hàm số f(x) xác định trên khoảng K chứa a. Hàm số f(x) liên tục tại x=a nếu
![]()

![]()
![]()
tìm m để hàm số liên tục trên R
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{3x^2-3x}{x-1}\\mx+1\end{matrix}\right.\) khi \(x\ne1\); khi \(x=1\)
Tìm m để các hàm số f ( x ) = x - 2 3 + 2 x - 1 x - 1 k h i x ≠ 1 3 m - 2 k h i x = 1 liên tục trên R.
Tìm a để các hàm số f ( x ) 3 x + 1 - 2 x 2 - 1 K h i x > 1 a ( x 2 - 2 ) x - 3 K h i x ≤ 1 liên tục tại x = 1
A. 1/2
B. 1/4
C. 3/4
D. 1
cho hàm số \(y=f\left(x\right)\) liên tục trên R thỏa
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=+\infty\) , \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=-\dfrac{1}{2}\)
tìm số đường tiệm cận củ đồ thị hàm số đã cho
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=+\infty\)