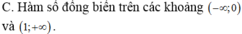Các câu hỏi tương tự
Cho hàm số y f(x) có
1
≤
f
(
x
)
≤
4
với mọi
x
∈
2
;
5
. Hỏi khẳng định nào dưới đây là khẳng định đúng? A.
3
≤
f
(
5
)
-
f
(
2
)
≤
12
B.
-
12
≤...
Đọc tiếp
Cho hàm số y = f(x) có 1 ≤ f ' ( x ) ≤ 4 với mọi x ∈ 2 ; 5 . Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. 3 ≤ f ( 5 ) - f ( 2 ) ≤ 12
B. - 12 ≤ f ( 5 ) - f ( 2 ) ≤ 3
C. 1 ≤ f ( 5 ) - f ( 2 ) ≤ 4
D. - 4 ≤ f ( 5 ) - f ( 2 ) ≤ - 1
Cho hàm số y f (x) có bảng biến thiên dưới đây. Khẳng định nào sau đây và khẳng định đúng? A. Đồ thị hàm số có 3 đường tiệm cận. B. Hàm số nghịch biến trên các khoảng
-
∞
;
0
và
0
;
+
∞
. C. Đồ thị hàm số không có tiệm cận. D. Hàm số...
Đọc tiếp
Cho hàm số y = f (x) có bảng biến thiên dưới đây.
Khẳng định nào sau đây và khẳng định đúng?
A. Đồ thị hàm số có 3 đường tiệm cận.
B. Hàm số nghịch biến trên các khoảng - ∞ ; 0 và 0 ; + ∞ .
C. Đồ thị hàm số không có tiệm cận.
D. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0.
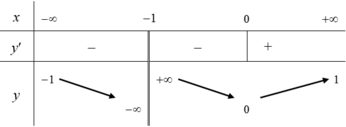
Cho hàm số yf(x) có bảng biến thiên dưới đây. Khẳng định nào sau đây và khẳng định đúng? A. Đồ thị hàm số có 3 đường tiệm cận. B. Hàm số nghịch biến trên các khoảng và . C. Đồ thị hàm số không có tiệm cận. D. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0.
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên dưới đây.
Khẳng định nào sau đây và khẳng định đúng?
A. Đồ thị hàm số có 3 đường tiệm cận.
B. Hàm số nghịch biến trên các khoảng ![]() và
và ![]() .
.
C. Đồ thị hàm số không có tiệm cận.
D. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0.
Cho hàm số
f
(
x
)
-
x
4
-
1
.
Khẳng định nào dưới đây đúng? A. Hàm không có điểm cực trị B. Hàm có một điểm cực tiểu và không có điểm cực đại C. Hàm có một điểm cực đại và không có điểm cực tiểu D. Hàm có một điểm cực tiểu và một điểm cực đại
Đọc tiếp
Cho hàm số f ( x ) = - x 4 - 1 . Khẳng định nào dưới đây đúng?
A. Hàm không có điểm cực trị
B. Hàm có một điểm cực tiểu và không có điểm cực đại
C. Hàm có một điểm cực đại và không có điểm cực tiểu
D. Hàm có một điểm cực tiểu và một điểm cực đại
Cho hàm số y f(x) có đạo hàm liên tục trên R Đồ thị hàm số y f’(x) như hình bên dưới Đặt g(x) f(x) - x khẳng định nào sau đây là đúng? A. g(2) g( -1) g(1) B. g( -1) g(1) g(2) C. g(-1) g( 1) g( 2) D. g( 1) g( -1) g( 2)
Đọc tiếp
Cho hàm số y= f(x) có đạo hàm liên tục trên R Đồ thị hàm số y= f’(x) như hình bên dưới
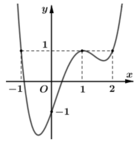
Đặt g(x) = f(x) - x khẳng định nào sau đây là đúng?
A. g(2) < g( -1) < g(1)
B. g( -1) < g(1) < g(2)
C. g(-1) > g( 1) > g( 2)
D. g( 1) < g( -1) < g( 2)
Cho hàm số y f(x) có đạo hàm liên tục trên R, đồ thị hàm y f’(x) như hình vẽ dưới đây. Khẳng định nào trong các phương án A, B, C, D dưới đây là đúng? A. . B. . C. . D. .
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên R, đồ thị hàm y = f’(x) như hình vẽ dưới đây. Khẳng định nào trong các phương án A, B, C, D dưới đây là đúng?
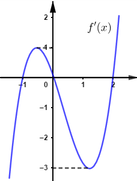
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y f(x) có
lim
x
→
+
∞
f
x
1
và
lim
x
→
-
∞
f
x
1
Trong các khẳng định dưới đây, khẳng định nào là đúng? A. Đồ thị hàm số không có tiệm cận ngang. B. Đồ thị hàm số có đúng một tiệm cận ngang. C. Đồ thị hàm số có hai tiệm cận ngang là y...
Đọc tiếp
Cho hàm số y = f(x) có lim x → + ∞ f x = 1 và lim x → - ∞ f x = 1
Trong các khẳng định dưới đây, khẳng định nào là đúng?
A. Đồ thị hàm số không có tiệm cận ngang.
B. Đồ thị hàm số có đúng một tiệm cận ngang.
C. Đồ thị hàm số có hai tiệm cận ngang là y = 1 và y = -1
D. Đồ thị hàm số có hai tiệm cận ngang là x = 1 và x = -1
Cho f(x), g(x) là hai hàm số liên tục trên K và a, b, c là ba số bất kỳ thuộc K. Khẳng định nào dưới đây là khẳng định đúng?
Đọc tiếp
Cho f(x), g(x) là hai hàm số liên tục trên K và a, b, c là ba số bất kỳ thuộc K. Khẳng định nào dưới đây là khẳng định đúng?
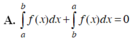
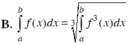
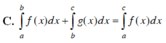
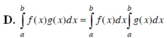
Cho hàm số y f(x) xác định trên M và có đạo hàm
f
(
x
)
x
+
2
x
-
1
2
Khẳng định nào sau đây là khẳng định đúng? A. Hàm số đồng biến trên B. Hàm số đạt cực đại tại C. Hàm số đạt cực đại tiểu D. Hàm số nghịch biến...
Đọc tiếp
Cho hàm số y = f(x) xác định trên M và có đạo hàm f ' ( x ) = x + 2 x - 1 2 Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số ![]() đồng biến trên
đồng biến trên ![]()
B. Hàm số ![]() đạt cực đại tại
đạt cực đại tại ![]()
C. Hàm số ![]() đạt cực đại tiểu
đạt cực đại tiểu ![]()
D. Hàm số ![]() nghịch biến trên
nghịch biến trên ![]()