Các câu hỏi tương tự
Cho hàm số: 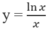 Chọn khẳng định đúng.
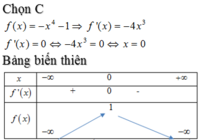
Chọn khẳng định đúng.
A. Hàm số có một cực tiểu
B. Hàm số có một cực đại
C. Hàm số không có cực trị
D. Hàm số có một cực đại và một cực tiểu
Cho hàm số: y = lnx x Chọn khẳng định đúng.
A. Hàm số có một cực tiểu
B. Hàm số có một cực đại
C. Hàm số không có cực trị
D. Hàm số có một cực đại và một cực tiểu
Cho hàm số y = - x 4 + 4 x 2 - 3. Khẳng định nào sau đây là đúng?
A. Hàm số có một cực đại và một cực tiểu
B. Hàm số có hai cực đại và một cực tiểu
C. Hàm số chỉ có một cực tiểu
D. Hàm số chỉ có một cực đại
Cho hàm số y = - x 4 + 4 x 2 - 3. Khẳng định nào sau đây là đúng?
A. Hàm số có một cực đại và một cực tiểu
B. Hàm số có hai cực đại và một cực tiểu
C. Hàm số chỉ có một cực tiểu
D. Hàm số chỉ có một cực đại
Trong các hàm số sau, hàm số nào có hai điểm cực đại và một điểm cực tiểu? A. y x4 – x2 + 3 B. y -x4 – x2 + 3 C. y -x4 + x2 + 3 D. y x4 + x2 + 3
Đọc tiếp
Trong các hàm số sau, hàm số nào có hai điểm cực đại và một điểm cực tiểu?
A. y = x4 – x2 + 3
B. y = -x4 – x2 + 3
C. y = -x4 + x2 + 3
D. y = x4 + x2 + 3
Cho hàm số yf(x) xác định và liên tục trên toàn trục số, hàm số f(x) có một điểm cực đại, một điểm cực tiểu với
f
C
Đ
3
;
f
C
T
1
. Biết
l
i
m
x
→
-
∞...
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên toàn trục số, hàm số f(x) có một điểm cực đại, một điểm cực tiểu với f C Đ = 3 ; f C T = 1 . Biết l i m x → - ∞ f ( x ) = - ∞ ; l i m x → + ∞ = + ∞ . Hỏi đồ thị (C) cắt trục hoành tại mấy điểm?
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị của m để đồ thị hàm số y
(
m
2
-
1
)
x
4
+
m
x
2
+
m
-
2
chỉ có một điểm cực đại và không có điểm cực tiểu. A. -1,5 m
≤
0 B. m
≤
1 C. -1
≤
m
≤...
Đọc tiếp
Tìm tất cả các giá trị của m để đồ thị hàm số y = ( m 2 - 1 ) x 4 + m x 2 + m - 2 chỉ có một điểm cực đại và không có điểm cực tiểu.
A. -1,5 < m ≤ 0
B. m ≤ 1
C. -1 ≤ m ≤ 0
D. -1 < m < 0,5
Cho hàm số y x4- 2( 1-m2) x2+ m+1. Tồn tại giác trị của m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất . Khi đó khẳng định nào đúng? A. m là số nguyên dương B. m không là số nguyên C. m 1 D. Tất cả sai
Đọc tiếp
Cho hàm số y= x4- 2( 1-m2) x2+ m+1. Tồn tại giác trị của m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất . Khi đó khẳng định nào đúng?
A. m là số nguyên dương
B. m không là số nguyên
C. m= 1
D. Tất cả sai
Tìm tất cả giá trị thực của m để hàm số y=x^4-2(m^2-m+1)x^2+m-1 có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu là ngắn nhất.
Cho hàm số yx4-2( m2-m+1)x2+m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất. A. m -1/2 B. m 1/2 C. m2 D. m1
Đọc tiếp
Cho hàm số y=x4-2( m2-m+1)x2+m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất.
A. m= -1/2
B. m= 1/2
C. m=2
D. m=1