Đáp án D.
Phương pháp:
∫ f " x . f ' x d x = f n + 1 x n + 1 + C , n ≠ − 1
Cách giải:
Ta có:
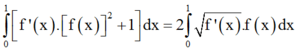
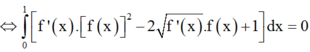


![]()
(do f x và f ' x đều nhận giá trị dương trên đoạn 0 ; 1 )


Mà
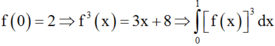

= 1 3 121 2 − 2 = 1 3 . 117 2 = 19 2
Đáp án D.
Phương pháp:
∫ f " x . f ' x d x = f n + 1 x n + 1 + C , n ≠ − 1
Cách giải:
Ta có:
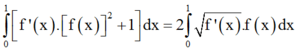
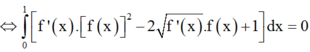


![]()
(do f x và f ' x đều nhận giá trị dương trên đoạn 0 ; 1 )


Mà
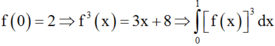

= 1 3 121 2 − 2 = 1 3 . 117 2 = 19 2
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0;1], f(x) và f' (x) đều nhận giá trị dương trên đoạn [0;1] và thỏa mãn f(0)=2, ∫ 0 1 f ' ( x ) . [ f ( x ) ] 2 + 1 ] dx = 2 ∫ 0 1 f ' ( x ) . f ( x ) dx . Tính ∫ 0 1 [ f ( x ) ] 3 dx ?
A. 15/4.
B. 15/2.
C. 17/2.
D. 19/2.
Cho hàm số f (x) nhận giá trị dương, có đạo hàm liên tục trên khoảng ( 0 ; + ∞ ) thỏa mãn 2 f ' ( x ) ( f ( x ) ) 2 = f ( x ) ( x + 2 ) x 3 , ∀ x > 0 và f ( 1 ) = 1 3 . Tích phân ∫ 1 2 1 ( f ( x ) ) 2 d x bằng
A. 11 2 +ln2
B. - 1 2 +ln2
C. 3 2 +ln2
D. 7 2 +ln2
Cho hàm số f (x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;2] thoả mãn f(0)=3,f(2)=12 và ∫ 0 2 ( f ' ( x ) ) 2 f ( x ) d x = 6 . Tính f(1).
A. 27 4
B. 25 4
C. 9 2
D. 15 4
Cho hàm số f(x) có đạo hàm dương, liên tục trên đoạn [0; 1] thỏa mãn điều kiện f(0)=1 và 3 ∫ 0 1 [ ( f ' ( x ) . f ( x ) ) 2 + 1 9 ≤ 2 ∫ 0 1 f ' ( x ) . f ( x ) d x . Tính ∫ 0 1 [ f ( x ) ] 3
A. 3/2
B. 5/4
C. 5/6
D. 7/6
Cho hàm số f (x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;3] thoả mãn f(0)=2,f(3)=8 và ∫ 0 3 ( f ' ( x ) ) 2 f ( x ) d x = 8 3 . Tính f(2).
A. 50/9.
B. 49/9.
C. 47/9.
D. 52/9
Cho hàm số f (x) có đạo hàm cấp hai liên tục trên đoạn [0;1] thoả mãn [ f ' ( x ) ] 2 + f ( x ) f '' ( x ) ≥ 1 , ∀ x ∈ [ 0 ; 1 ] và f 2 ( 0 ) + f ( 0 ) . f ' ( 0 ) = 3 2 . Giá trị nhỏ nhất của tích phân ∫ 0 1 f 2 ( x ) d x bằng
A. 5 2
B. 1 2
C. 11 6
D. 7 2
Cho hàm số f(x) có đạo hàm dương, liên tục trên đoạn [0;1] thỏa mãn điều kiện f(0)=1 và 3 ∫ 0 1 [ ( f ' ( x ) . f ( x ) ) 2 + 1 9 ] d x ≤ 2 ∫ 0 1 f ' ( x ) . f ( x ) d x . Tính ∫ 0 1 [ f ( x ) ] 3
A. 3/2
B. 5/4
C. 5/6
D. 7/6
Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [-2;1] thỏa mãn f(0)=1 và f x 2 . f ' x = 3 x 2 + 4 x + 2 Giá trị lớn nhất của hàm số y=f(x) trên đoạn [-2;1] là
A. 2 16 3
B. 18 3
C. 16 3
D. 2 18 3
Cho hàm số y=f(x) liên tục, không âm trên R thỏa mãn f ( x ) . f ' ( x ) = 2 x f ( x ) 2 + 1 và f(0)=0. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y=f(x) trên đoạn [1;3] lần lượt là:
A. M=20;m=2
B. M = 4 11 ; m = 3
C. M = 20 ; m = 2
D. M = 3 11 ; m = 3
Cho hàm số f(x) có đạo hàm liên tục trên R và thỏa mãn f(x)>0,∀x∈R. Biết f(0)=1 và (2-x)f(x)-f' (x)=0. Tìm tất cả các giá trị thực của tham số m để phương trình f(x)=m có hai nghiệm phân biệt.
A. m< e 2 .
B. 0<m< e 2 .
C. 0<m≤ e 2 .
D. m > e 2