Question

Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d ( a , b , c , d ∈ ℝ )  có đồ thị như hình vẽ. Đồ thị hàm số g ( x ) = x 2 + 4 x + 3 x 2 + x x f x 2 - 2 f ( x )  có bao nhiêu đường tiệm cận đứng?

A. 3

B. 2

C. 6

D. 4

Answer 1

Điều kiện:

 

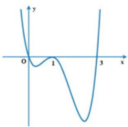
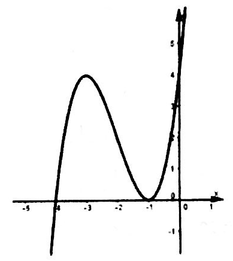
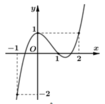
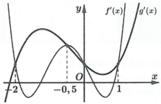
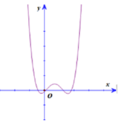
Từ đồ thị hàm số y=f(x) ta thấy phương trình f(x)=0 có nghiệm x=-3 (bội 2) và nghiệm đơn x = x 0 ∈ - 1 ; 0  nên ta viết lại f ( x ) = a x + 3 2 x - x 0  

Khi đó

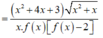
Dựa vào đồ thị ta cũng thấy, đường thẳng y=2 cắt đồ thị hàm số y=f(x) tại ba điểm phân biệt x=-1, x = x 1 ∈ - 3 ; - 1 , x = x 2 < - 3 nên ta viết lại

 

Khi đó

 

 

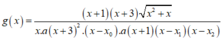
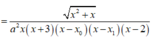
Dễ thấy x = x 0 ∈ - 1 ; 0  nên ta không xét giới hạn của hàm số tại điểm x 0   

Ta có:

+) l i m x → 0 + g ( x ) = l i m x → 0 +

 

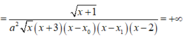
⇒ x = 0  là đường TCĐ của đồ thị hàm số y=g(x) 

+)  

⇒  Các đường thẳng x = - 3 , x = x 1 , x = x 2  đều là các đường tiệm cận đứng của đồ thị hàm số y=g(x)

Vậy đồ thị hàm số y=g(x) có tất cả 4 đường tiệm cận đứng.

Chọn đáp án D.