Đáp án C
Ta có y ' = 4 x ln 4 + 4 - x ln 4 2 ⇒ M = 1 2 4 x + 4 - x ln 4 + 1 2 4 x - 4 - x = 4 x ln 4 .
Đáp án C
Ta có y ' = 4 x ln 4 + 4 - x ln 4 2 ⇒ M = 1 2 4 x + 4 - x ln 4 + 1 2 4 x - 4 - x = 4 x ln 4 .
Cho hàm số y = ln ( x - 1 ) x 2 - m x + 4 . Để đồ thị có hai tiệm cận thì giá trị của m bằng
A. 5
B. 4
C. 2
D. 7
Cho đồ thị hàm số y = 1 2 ( x - 1 ) ( x 2 - 4 ) như hình vẽ bên. Số điểm cực trị của đồ thị hàm số f(x)=|(|x-1| ( x 2 - 4 ) +m)| , với m thuộc đoạn (2;6) là
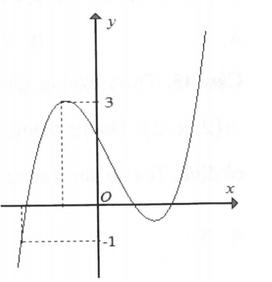
A. 6.
B. 3.
C. 7.
D. 5.
Cho hàm số y = 1 3 x 3 - ( m + 1 ) x 2 + ( m + 3 ) x + m - 4 . Tìm m để hàm số y=f(|x|) có 5 điểm cực trị
A. -3<m<-1
B. m>1
C. m>4
D. m>0
Tìm tham số thực m để hàm số y = f ( x ) = x 2 + x - 12 x + 4 k h i x k h a c - 4 m x + 1 k h i x = - 4 liên tục tại điểm x=-4
A. m=4
B. m=3
C. m=2
D. m=5
Cho hàm số y = f(x) liên tục trên R sao cho m a x x ∈ 0 ; 10 f ( x ) = f ( 2 ) = 4 . Xét hàm số g ( x ) = f ( x 3 + x ) − x 2 + 2 x + m . Giá trị của tham số m để m a x x ∈ 0 ; 2 g ( x ) = 8 là
A. 5
B. 4
C. -1
D. 3
Đường thẳng d: y=x+4 cắt đồ thị hàm số y = x 3 + 2 m x 2 + ( m + 3 ) x + 4 tại 3 điểm phân biệt A(0;4), B và C sao cho diện tích tam giác MBC bằng 4, với M(1;3). Mệnh đề nào sau đây là đúng?
A. m ∈ - ∞ ; 0
B. m ∈ 0 ; 2
C. m ∈ 2 ; 4
D. m ∈ 4 ; + ∞
Tìm tất cả các giá trị của m để đường thẳng d : y = x + 4 cắt đồ thị hàm số y = x 3 + 2 m x 2 + ( m + 3 ) x + 4 tại 3 điểm phân biệt A ( 0 ; 4 ) và C sao cho diện tích ∆ M B C bằng 4, với M(1;3)
A. m = 2 m = 3
B. m = - 2 m = 3
C. m = 3
D. m = - 3 m = - 2
Đường thẳng d : y = x + 4 cắt đồ thị hàm số y = x 3 + 2 m x 2 + ( m + 3 ) x + 4 tại 3 điểm phân biệt A(0;4) B và C sao cho diện tích tam giác MBC bằng 4, với M(1;3) Tìm tất cả các giá trị của m thỏa mãn yêu cầu bài toán
A. m=2 hoặc m=3
B. m=-2 hoặc m=3
C. m=3
D. m=-2 hoặc m=-3
Cho hàm số f ( x ) = x 4 + 2 m x 2 + m với m làm tham số, m>0
Đặt g ( x ) = f ( x ) + f ' ( x ) + f ' ' ( x ) + f ( 3 ) ( x ) + f ( 4 ) ( x ) Mệnh đề nào dưới đây đúng
A. g ( x ) ≥ 0 ∀ x
B. g ( x ) < 0 ∀ x
C. g ( x ) > 0 ∀ x
D. g ( x ) ≤ 0 ∀ x
Cho hàm số y = f ( x ) = x - m 2 x + 4 với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1
A. m = 2
B. m = 0
C. m 6
D. m = 3