Các câu hỏi tương tự
Đặt m log 2 và n log 7. Hãy biểu diễn
log
6125
7
theo m và n.
Đọc tiếp
Đặt m = log 2 và n = log 7. Hãy biểu diễn log 6125 7 theo m và n.
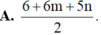
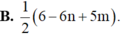
![]()
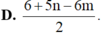
Cho
f
x
a
ln
x
+
x
2
+
1
+
b
sin
x
+
6
với
a
,
b
∈
ℝ
. Biết rằng f(log(log e)) 2. Tính giá trị của f(log(ln10)). A. 10 B. 2 C. 4 D. 8
Đọc tiếp
Cho f x = a ln x + x 2 + 1 + b sin x + 6 với a , b ∈ ℝ . Biết rằng f(log(log e)) = 2. Tính giá trị của f(log(ln10)).
A. 10
B. 2
C. 4
D. 8
1.Tính các giá trị biểu thức sau:a)510000.log52-59999.log52-...-53.log52-52.log52?b)(x2+1).4100000-(x2+1).499999,5-...-(x2+1).43.5-(x2+1).43?2.Giải ptrình bậc cao sau:a)x.(x2+y)150000-x.(x2+y)149999-...-x.(x2+y)2-x3-xy-20b)xy(2y+1)50000-xy(2y+1)49999-...-xy(2y+1)2-2xy2-30c)x2(x+1)10000-x2(x+1)9999-...-x2(x+1)2-x2(x+1)-x2-103.Tính giá trị tại vị trí gián đoạn sau:a)250000-249999-...-24-23?Biết gián đoạn tại vị trí thứ 4b)710000.log72-79999.log72-...-72.log72-7log72?Biết gián đoạn tại vị trí 3-5c)...
Đọc tiếp
1.Tính các giá trị biểu thức sau:
a)510000.log52-59999.log52-...-53.log52-52.log52=?
b)(x2+1).4100000-(x2+1).499999,5-...-(x2+1).43.5-(x2+1).43=?
2.Giải ptrình bậc cao sau:
a)x.(x2+y)150000-x.(x2+y)149999-...-x.(x2+y)2-x3-xy-2=0
b)xy(2y+1)50000-xy(2y+1)49999-...-xy(2y+1)2-2xy2-3=0
c)x2(x+1)10000-x2(x+1)9999-...-x2(x+1)2-x2(x+1)-x2-1=0
3.Tính giá trị tại vị trí gián đoạn sau:
a)250000-249999-...-24-23=?Biết gián đoạn tại vị trí thứ 4
b)710000.log72-79999.log72-...-72.log72-7log72=?Biết gián đoạn tại vị trí 3->5
c)22+23+...+24999+25000=?Biết gián đoạn tại vị trí thứ 350 và vị trí 600
4.Thực hiện các yêu cầu sau:
Cho pt M: x.(x+1)50000-x.(x+1)49999-...-x.(x+1)3-x.(x+1)2-n=0
a.Xác định x=?
b.Tính n=?
c.Số nào dưới đây là số nguyên tố là:
A.n+1/n-1
B.n+2/n-2
C.n+3/n-3
D.n+4/n-4
Cho dãy số
(
u
n
)
thỏa mãn
log
u
1
+
2
+
log
u
1
-
2
log
u
10
2
log
u...
Đọc tiếp
Cho dãy số ( u n ) thỏa mãn log u 1 + 2 + log u 1 - 2 log u 10 = 2 log u 10
và u n + 1 = 2 u n với mọi n ≥ 1 Giá trị nhỏ nhất của n đề u n > 5 100 bằng
A. 247
B. 248
C. 229
D. 290
Cho dãy số (un) thỏa mãn
log
u
1
+
2
+
log
u
1
-
2
log
u
10
2
log
u
10...
Đọc tiếp
Cho dãy số (un) thỏa mãn log u 1 + 2 + log u 1 - 2 log u 10 = 2 log u 10 và un+1 = 2un với mọi n ≥ 1 . Giá trị nhỏ nhất của n để un > 5100 bằng
A. 247.
B. 248.
C. 229.
D. 290.
Cho hàm số
y
ln
2
x
-
a
-
2
m
ln
2
x
-
a
+
2
(m là tham số thực), trong đó x,...
Đọc tiếp
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 x 2 + a 2 - 2 n - 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 , e 2 y = 1 . Số phần tử của S là:
A. 0
B. 1
C. 2
D. Vô số
Cho hàm số
y
ln
(
2
x
-
a
)
-
2
m
ln
(
2
x
-
a
)
+...
Đọc tiếp
Cho hàm số y = ln ( 2 x - a ) - 2 m ln ( 2 x - a ) + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + . . . + log . . . 2 ( x 2 + a 2 ) - ( 2 n + 1 - 1 ) ( log 2 x a + 1 ) = 0
(với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thoả mãn m a x [ 1 ; e 2 ] y = 1 . Số phần tử của S là
A. 0
B. 1
C. 2
D. Vô số
Tính giá trị của biểu thức sau: \(log^2_{\dfrac{1}{a}}a^2+log_{a^2}a^{\dfrac{1}{2}}\) (1≠a>0)
A. \(\dfrac{17}{4}\)
B. \(\dfrac{13}{4}\)
C. \(-\dfrac{11}{4}\)
D. -\(\dfrac{15}{4}\)
có bao nhiêu giá trị nguyên của m để phương trình \(\left(x-1\right)\log\left(e^{-x}+m\right)=x-2\) có 2 nghiệm thực phân biêt







