Các câu hỏi tương tự
Cho hai số phức
z
1
,
z
2
thỏa mãn
|
z
1
|
|
z
2
|
|
z
1
+
z
2
|
1
.
Khi đó
|
z
1
-
z...
Đọc tiếp
Cho hai số phức z 1 , z 2 thỏa mãn | z 1 | = | z 2 | = | z 1 + z 2 | = 1 . Khi đó | z 1 - z 2 | bằng
A. 0
B. 1
C. 2
D. 3
Cho hai số phức
z
1
,
z
2
thỏa mãn
|
z
1
|
|
z
2
|
1
,
|
z
1
+
z
2
|
13
. Khi đó
|
z
1
...
Đọc tiếp
Cho hai số phức z 1 , z 2 thỏa mãn | z 1 | = | z 2 | = 1 , | z 1 + z 2 | = 13 . Khi đó | z 1 - z 2 | bằng:
A. 0
B. 1
C. 2
D. 3
Gọi T là tập hợp các số phức z thỏa mãn
z
-
i
≥
3
và
z
-
1
≤
5
. Gọi
z
1
,...
Đọc tiếp
Gọi T là tập hợp các số phức z thỏa mãn z - i ≥ 3 và z - 1 ≤ 5 . Gọi z 1 , z 2 ∈ T lần lượt là các số phức có môdun nhỏ nhất và lớn nhất. Tìm số phức z 1 + 2 z 2
A. 12+2i
B. -2+12i
C. 6-4i
D. 12+4i
Cho hai số phức
z
1
-
3
+
4
i
,
z
2
4
-
3
i
.
Môđun của số phức
z
z
1
+
z
2
+
z
1
.
z...
Đọc tiếp
Cho hai số phức z 1 = - 3 + 4 i , z 2 = 4 - 3 i . Môđun của số phức z = z 1 + z 2 + z 1 . z 2 là
A. 27
B. 27
C. 677
D. 677
Cho hai số phức
z
1
1
+
2
i
,
z
2
2
-
3
i
.
Phần thực và phần ảo của số phức
w
3
z
1
-
2
z
2
là A. 1 và 12 B. -1 và 12 C. –1 và 12i D...
Đọc tiếp
Cho hai số phức z 1 = 1 + 2 i , z 2 = 2 - 3 i . Phần thực và phần ảo của số phức w = 3 z 1 - 2 z 2 là
A. 1 và 12
B. -1 và 12
C. –1 và 12i
D. 1 và 12i
Cho phương trình z^2+bc+c0 có hai nghiệm z1 z2 thỏa mãn z2 - z1 4+2i . Gọi A,B là các điểm biểu diễn các nghiệm của phương trình z^2-2bz+4c0 . Tính độ dài đoạn ABA: 8sqrt{5}B: 2sqrt{5}C: 4sqrt{5}D: sqrt{5}
Đọc tiếp
Cho phương trình \(z^2+bc+c=0\) có hai nghiệm z1 z2 thỏa mãn z2 - z1 = 4+2i . Gọi A,B là các điểm biểu diễn các nghiệm của phương trình \(z^2-2bz+4c=0\) . Tính độ dài đoạn AB
A: \(8\sqrt{5}\)
B: \(2\sqrt{5}\)
C: \(4\sqrt{5}\)
D: \(\sqrt{5}\)
Cho số phức z thỏa mãn
5
(
z
+
i
)
z
+
1
2
-
i
.
Khi đó môđun của số phức
w
1
+
z
+
z
2
là A. 5 B.
13
C. 13 D.
5
Đọc tiếp
Cho số phức z thỏa mãn 5 ( z + i ) z + 1 = 2 - i . Khi đó môđun của số phức w = 1 + z + z 2 là
A. 5
B. 13
C. 13
D. 5
Cho
z
x
+
y
i
với x, y
∈
R
là số phức thỏa mãn điều kiện
z
¯
+
2
-
3
i
≤
|
z
+
i
-
2
|
≤
5
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ...
Đọc tiếp
Cho z = x + y i với x, y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ | z + i - 2 | ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 x . Tính M+m.
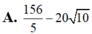
![]()
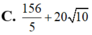
![]()
Cho số phức z thỏa mãn: i . z + z = 2 + 2 i và z . z = 2 . Khi đó z 2 bằng:
A. 2
B. 4
C. – 2i
D. 2i


