Các câu hỏi tương tự
Cho đường thẳng d song song với mặt phẳng (∝), mặt phẳng (β) chứa d và cắt (∝) theo giao tuyến d’. Khẳng định nào sau đây là đúng ?
A. d’ // d hoặc d’ ≡ d
B. d’ // d
C. d’ ≡ d
D. d’ và d chéo nhau
Cho đường thẳng d song song mặt phẳng
(
α
)
nằm trong mặt phẳng
(
β
)
. Gọi a là giao tuyến của
(
α
)
và
(
β
)
Khi đó A. a và d trùng nhau. B. a và d cắt nhau. C. a song song d. D. a và d chéo nhau.
Đọc tiếp
Cho đường thẳng d song song mặt phẳng ( α ) nằm trong mặt phẳng ( β ) . Gọi a là giao tuyến của ( α ) và ( β ) Khi đó
A. a và d trùng nhau.
B. a và d cắt nhau.
C. a song song d.
D. a và d chéo nhau.
Số phát biểu đúng 1. Trong không gian qua 1 điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho 2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy đồng quy 3. Nếu 2 mặt phẳng phân biệt lần lượt chứa 2 đường thẳng song song thì giao tuyến của chúng ( nếu có ) cũng song song với 2 đường thẳng đó hoặc trùng với một trong 2 đường thẳng đó 4. 2 đường thẳng phân biệt cùng song song với đường thẳng th...
Đọc tiếp
Số phát biểu đúng
1. Trong không gian qua 1 điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy đồng quy
3. Nếu 2 mặt phẳng phân biệt lần lượt chứa 2 đường thẳng song song thì giao tuyến của chúng ( nếu có ) cũng song song với 2 đường thẳng đó hoặc trùng với một trong 2 đường thẳng đó
4. 2 đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì chúng song song với nhau
5. Nếu đường thẳng d không nằm trong mặt phẳng ( ) và d song song với đường thẳng d’ nằm trong ( ) thì d song song với ( )
6. Cho đường thẳng a song song với mặt phẳng . Nếu mặt phẳng chứa a và cắt theo giao tuyến b thì b song song với a
7. Nếu 2 mặt phẳng cùng song song với 1 đường thẳng thì giao tuyến của chúng ( nếu có ) cũng song song với đường thẳng đó
8. Cho 2 đường thẳng chéo nhau. Có vô số mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
A. 8
B. 7
C. 6
D. 5
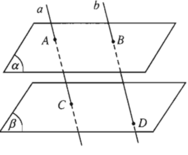
Cho hai mặt phẳng (α) và (β) song song với nhau. Đường thẳng a cắt (α) và (β) lần lượt tại A và C. Đường thẳng b song song với a cắt (α) và (β) lần lượt tại B và D.
Hình 2.72 minh họa nội dung trên đúng hay sai?
Trong các khẳng định sau đây khẳng định nào đúng? khẳng định nào sai?a) Cho hai đường thẳng a và b song song với nhau. Nếu có một đường thẳng d vuông góc với a thì d vuông góc với b.b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song với nhau.c) Một mặt phẳng (α) và một đường thẳng a cùng vuông góc với đường thằng b thì a // (α).d) Hai mặt phẳng (α) và (β) phân biệt cùng vuông góc với một mặt phẳng (γ) thì (α) // (β).e) Hai đường thẳng phân biệt cùng vuông góc với m...
Đọc tiếp
Trong các khẳng định sau đây khẳng định nào đúng? khẳng định nào sai?
a) Cho hai đường thẳng a và b song song với nhau. Nếu có một đường thẳng d vuông góc với a thì d vuông góc với b.
b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song với nhau.
c) Một mặt phẳng (α) và một đường thẳng a cùng vuông góc với đường thằng b thì a // (α).
d) Hai mặt phẳng (α) và (β) phân biệt cùng vuông góc với một mặt phẳng (γ) thì (α) // (β).
e) Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song với nhau.
f) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song.
Cho hai mặt phẳng (P), (Q) cắt nhau theo giao tuyến là đường thẳng d . Đường thẳng a song song với cả hai mặt phẳng (P), (Q). Khẳng định nào sau đây đúng? A. a,d trùng nhau B. a,d chéo nhau C. a song song d D. a,d cắt nhau
Đọc tiếp
Cho hai mặt phẳng (P), (Q) cắt nhau theo giao tuyến là đường thẳng d . Đường thẳng a song song với cả hai mặt phẳng (P), (Q). Khẳng định nào sau đây đúng?
A. a,d trùng nhau
B. a,d chéo nhau
C. a song song d
D. a,d cắt nhau
Cho tam giác ABC. Gọi (α) là mặt phẳng vuông góc với đường thẳng CA tại A và (β) là mặt phẳng vuông góc với đường thẳng CB tại B. Chứng minh rằng hai mặt phẳng (α) và (β) cắt nhau và giao tuyến d của chúng vuông góc với mặt phẳng (ABC).
Cho hai mặt phẳng (α) và (β) vuông góc với nhau và cắt nhau theo giao tuyến d. Chứng minh rằng nếu có một đường thẳng Δ nằm trong (α) và Δ vuông góc với d thì Δ vuông góc với (β)
Cho hai đường thẳng a, b cố định, song song với nhau và khoảng cách giữa chúng bằng 4. Hai mặt phẳng (P), (Q) thay đổi vuông góc với nhau lần lượt chứa hai đường thẳng a, b. Gọi d là giao tuyến của (P), (Q). Khẳng định nào sau đây là đúng? A. d thuộc 1 mặt trụ cố định có khoảng cách giữa đường sinh và trục bằng 4 B. d thuộc 1 mặt nón cố định C. d thuộc 1 mặt trụ cố định có khoảng cách giữa đường sinh và trục bằng 2
2
D. d thuộc 1 mặt trụ cố định có khoảng c...
Đọc tiếp
Cho hai đường thẳng a, b cố định, song song với nhau và khoảng cách giữa chúng bằng 4. Hai mặt phẳng (P), (Q) thay đổi vuông góc với nhau lần lượt chứa hai đường thẳng a, b. Gọi d là giao tuyến của (P), (Q). Khẳng định nào sau đây là đúng?
A. d thuộc 1 mặt trụ cố định có khoảng cách giữa đường sinh và trục bằng 4
B. d thuộc 1 mặt nón cố định
C. d thuộc 1 mặt trụ cố định có khoảng cách giữa đường sinh và trục bằng 2 2
D. d thuộc 1 mặt trụ cố định có khoảng cách giữa đường sinh và trục bằng 2



