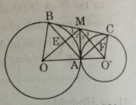
MA và MB là các tiếp tuyến của (O) (gt).
Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
MA = MB
MO là tia phân giác của góc AMB
ΔAMB cân tại M (MA = MB) mà có MO là đường phân giác nên đồng thời là đường cao
=> MO ⊥ AB hay ∠MEA = 90o
Tương tự ta có MO' là tia phân giác của góc AMC và ∠MFA = 90o
MO, MO' là tia phân giác của hai góc kề bù ∠AMB và ∠AMC nên ∠EMF = 90o
=> Tứ giác AEMF là hình chữ nhật (vì có ba góc vuông).









