Chọn đáp án A
Gọi (P) là mặt phẳng tạo bởi đường thẳng a và M ; (Q) là mặt phẳng tạo bởi đường thẳng b và M.
Giả sử c là đường thẳng đi qua M, c cắt cả a và b.
Suy ra
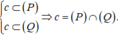
Vậy chỉ có một đường thẳng đi qua M cắt cả a và b.
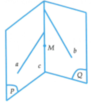
Chọn đáp án A
Gọi (P) là mặt phẳng tạo bởi đường thẳng a và M ; (Q) là mặt phẳng tạo bởi đường thẳng b và M.
Giả sử c là đường thẳng đi qua M, c cắt cả a và b.
Suy ra
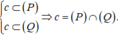
Vậy chỉ có một đường thẳng đi qua M cắt cả a và b.

Cho mặt trụ (T) và một điểm S cố định nằm ngoài (T). Một đường thẳng Δ luôn đi qua S và cắt (T) tại hai điểm A, B (A, B có thể trùng nhau). Gọi M là trung điểm của đoạn thẳng AB. Tập hợp các điểm M là
A. Một mặt phẳng đi qua S.
B. Một mặt cầu đi qua S.
C. Một mặt nón có đỉnh là S.
D. Một mặt trụ.
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn C : x + 1 2 + y - 2 2 = 9 và điểm I - 3 ; 3 . Đường thẳng ∆ : a x + b + c = 0 đi qua điểm I và cắt đường tròn (C) tại hai điểm A và B. Tiếp tuyến của A và B cắt nhau tại M. Biết điểm M thuộc đường thẳng x + 3 y - 4 = 0 . Tính P = 2 a + 3 b c
A. P = 1 3
B. P = - 11 4
C. P = 2 3
D. P = 1 4
Trong mặt phẳng Oxy, cho đường tròn (C): x 2 + y 2 - 2 x - 6 y + 6 = 0 . Đường thẳng (d) đi qua M(2;3) cắt (C) tại hai điểm A, B. Tiếp tuyến của đường tròn tại A và cắt nhau tại E. Biết S A E B = 32 5 và phương trình đường thẳng (d) có dạng a x - y + c = 0 với a , c ∈ ℤ , a > 0 . Khi đó a + 2 c bằng:
A. 1
B. -1
C. -4
D. 0
Cho ba điểm A, B, C nằm ngoài đường thẳng a. Biết rằng cả hai đoạn thẳng BA, BC đều cắt đường thẳng a. Hỏi đoạn thẳng AC có cắt đường thẳng a hay không ? Vì sao ?
Gọi tên hai nửa mặt phẳng đối nhau bờ a.
Cho d là đường thẳng đi qua điểm A - 1 ; 3 và có hệ số góc m. Gọi S là tập hợp các giá trị của tham số m để đường thẳng d cắt đồ thị C của hàm số y = x 3 - 3 x + 1 tại ba điểm phân biệt A, B, C sao cho tiếp tuyến với đồ thị tại B và C cắt nhau tại điểm I nằm trên đường tròn đường kính BC. Tính tổng bình phương các phần tử thuộc tập hợp S.
A. 16 9
B. 34 9
C. 38 9
D. 34 3
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x - 2 1 = y - 5 2 = z - 2 1 , d ' : x - 2 1 = y - 1 - 2 = z - 2 1 và hai điểm A(a;0;0), A’(0;0;b). Gọi (P) là mặt phẳng chứa d và d’; H là giao điểm của đường thẳng AA’ và mặt phẳng (P). Một đường thẳng thay đổi trên (P) nhưng luôn đi qua H đồng thời D cắt d và d’ lần lượt tại B, B’. Hai đường thẳng AB, A’B’ cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có vectơ chỉ phương u → = 15 ; - 10 ; - 1 (tham khảo hình vẽ). Tính a+b
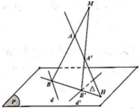
A. 8
B. 9
C. -9
D. 6
Cho hàm số y = x 3 - 2 ( m + 1 ) x 2 + ( 5 m + 1 ) x - 2 m - 2 có đồ thị là (Cm) với m là tham số. Có bao nhiêu giá trị của m nguyên trong đoạn [–10;100] để (Cm) cắt trục hoành tại ba điểm phân biệt A(2;0), B, C sao cho trong hai điểm B, C có một điểm nằm trong và một điểm nằm ngoài đường tròn có phương trình x2 + y2 = 1?
A. 109
B. 108
C. 18
D. 19
Trong không gian cho hai đường thẳng a và b cắt nhau. Đường thẳng c cắt cả hai đường a và b. Có bao nhiêu mệnh đề sai trong các mệnh đề sau
(I) a, b, c luôn đồng phẳng
(II) a, b đồng phẳng
(III) a, c đồng phẳng
A. 0
B. 1
C. 2
D. 3
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x − 2 1 = y − 5 2 = z − 2 1 , d ' : x − 2 1 = y − 1 − 2 = z − 2 1 và hai điểm A a ; 0 ; 0 , A ' 0 ; 0 ; b . Gọi (P) là mặt phẳng chứa d và d¢; H là giao điểm của đường thẳng AA¢ và mặt phẳng (P). Một đường thẳng D thay đổi trên (P) nhưng luôn đi qua H đồng thời D cắt d và d¢ lần lượt tại B, B¢. Hai đường thẳng A B , A ' B ' cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có véc tơ chỉ phương u → 15 ; − 10 ; − 1 (tham khảo hình vẽ). Tính T = a + b

A. T = 8
B. T = 9
C. T = - 9
D. T = 6