Các câu hỏi tương tự
Cho hai điểm A, B thuộc đồ thị hàm số y = - x 3 + 3 x + 2 (C) đối xứng nhau qua điểm I(-1;3). Tọa độ điểm A là:
A. A(1;4)
B. A(-1;0)
C. Không tồn tại
D. A(0;2)
Có hai điểm A, B phân biệt thuộc đồ thị hàm số
C
:
y
x
+
2
x
-
1
sao cho A và B đối xứng với nhau qua điểm M(3;3). Tính độ dài đoạn thẳng AB. A.
A
B
2
2
B.
A
B
5
2
C. ...
Đọc tiếp
Có hai điểm A, B phân biệt thuộc đồ thị hàm số C : y = x + 2 x - 1 sao cho A và B đối xứng với nhau qua điểm M(3;3). Tính độ dài đoạn thẳng AB.
A. A B = 2 2
B. A B = 5 2
C. A B = 6 2
D. A B = 3 2
Cho (C) là đồ thị của hàm số
y
x
-
3
x
+
1
.
Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN. A. I(-1;1) B.
I
0
;
-...
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 . Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN.
A. I(-1;1)
B. I 0 ; - 3 2
C. I 0 ; 3 2
D. I(-2;2)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + y + z - 3 = 0 và cho điểm A(1; 2; 3). Tìm tọa độ của điểm B đối xứng với A qua (P)
A. B(-1; 0; 1)
B. B(1; -1; 0)
C. B(-1; -1; -1)
D. B(1; -2; 1)
Giả sử
m
-
a
b
,
a
,
b
∈
Z
+
,
(
a
,
b
)
1
là giá trị thực của tham số m để đường thẳng
d
:
y
-
3
x
+
m
cắt đồ thị hàm số
y
2
a...
Đọc tiếp
Giả sử m = - a b , a , b ∈ Z + , ( a , b ) = 1 là giá trị thực của tham số m để đường thẳng d : y = - 3 x + m cắt đồ thị hàm số y = 2 a + 1 x - 1 tại hai điểm phân biệt A,B sao cho trọng tâm tam giác OAB thuộc đường thẳng ∆ : x - 2 y - 2 = 0 với O là gốc tọa độ. Tính a+2b
A. 2
B. 5
C. 11
D. 21
Cho hàm số
y
x
+
1
x
-
1
có đồ thị (C). Giả sử A, B là hai điểm thuộc (C) và đối xứng nhau qua giao điểm của hai đường tiệm cận. Dựng hình vuông AEBF. Tìmdiện tích nhỏ nhất của hình vuông AEBF. A.
S
m
i
n
8...
Đọc tiếp
Cho hàm số y = x + 1 x - 1 có đồ thị (C). Giả sử A, B là hai điểm thuộc (C) và đối xứng nhau qua giao điểm của hai đường tiệm cận. Dựng hình vuông AEBF. Tìmdiện tích nhỏ nhất của hình vuông AEBF.
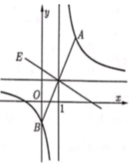
A. S m i n = 8 2
B. S m i n = 4 2
C. S m i n = 8
D. S m i n = 16
Đường thẳng d: yx+m cắt đồ thị hàm số
y
x
-
1
x
+
1
tại hai điểm phân biệt A, B sao cho
O
A
2
+
O
B
2
2
, O là gốc tọa độ. Khi đó m thuộc khoảng A.
-
∞...
Đọc tiếp
Đường thẳng d: y=x+m cắt đồ thị hàm số y = x - 1 x + 1 tại hai điểm phân biệt A, B sao cho O A 2 + O B 2 = 2 , O là gốc tọa độ. Khi đó m thuộc khoảng
A. - ∞ ; 2 - 2 2
B. 0 ; 2 + 2 2
C. 2 + 2 ; 2 + 2 2
D. 2 + 2 2 ; + ∞
ChoA(1 ;2 ;3),B(-4 ;0 ;1) , C(-2 ;3 ;1)vàD(-3 ;2 ;-1). Tọa độ điểm A’ đối xứng với A qua mặt phẳng (BCD) là A.
A
-
17
47
;
16
47
;
19
47
B.
A
-
187
53...
Đọc tiếp
ChoA(1 ;2 ;3),B(-4 ;0 ;1) , C(-2 ;3 ;1)vàD(-3 ;2 ;-1). Tọa độ điểm A’ đối xứng với A qua mặt phẳng (BCD) là
A. A ' - 17 47 ; 16 47 ; 19 47
B. A ' - 187 53 ; 160 53 ; 199 53
C. A ' - 187 53 ; 266 53 ; 199 53
D. A ' 17 47 ; - 16 47 ; - 19 47
Tìm cặp điểm thuộc đồ thị (C) của hàm số
y
x
+
2
x
+
1
đối xứng nhau qua gốc tọa độ. A.
2
;
2
và
−
2
;...
Đọc tiếp
Tìm cặp điểm thuộc đồ thị (C) của hàm số y = x + 2 x + 1 đối xứng nhau qua gốc tọa độ.
A. 2 ; 2 và − 2 ; − 2
B. 3 ; − 2 và − 3 ; 2
C. 2 ; − 2 và − 2 ; 2
D. (2;-2và (-2;2)