Các câu hỏi tương tự
Cho (H) là hình phẳng nằm bên trong nửa elip
y
1
2
4
-
x
2
và nằm bên ngoài parabol
y
3
2
x
2
Diện tích của (H) bằng A.
4
π
-
3
6...
Đọc tiếp
Cho (H) là hình phẳng nằm bên trong nửa elip y = 1 2 4 - x 2 và nằm bên ngoài parabol y = 3 2 x 2 Diện tích của (H) bằng
A. 4 π - 3 6
B. 2 π + 3 6
C. 2 π - 3 6
D. 4 π + 3 6
Tìm góc
α
∈
{π/6;π/4;π/3;π/2} để phương trình cos2x+
3
sin2x-2cosx 0 tương đương với phương trình c
o
s
(
2
x
-
α
)
cos
x
A.
α
π
/
6
B.
α
π
/
4
C.
α
π
/
2...
Đọc tiếp
Tìm góc α ∈ {π/6;π/4;π/3;π/2} để phương trình cos2x+ 3 sin2x-2cosx= 0 tương đương với phương trình c o s ( 2 x - α ) = cos x
A. α = π / 6
B. α = π / 4
C. α = π / 2
D. α = π / 3
Cho (H) là hình phẳng giới hạn bởi parabol
y
3
2
x
2
và nửa đường elip có phương trình
y
1
2
4
-
x
2
(
v
ớ
i
-
2
≤
x
≤
2
)
(phần tô đậm trong...
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 2 x 2 và nửa đường elip có phương trình y = 1 2 4 - x 2 ( v ớ i - 2 ≤ x ≤ 2 ) (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
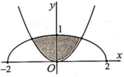
A. 2 π + 3 6
B. 2 π + 3 12
C. 2 π - 3 6
D. 4 π + 3 6
Cho hai điểm A, B thuộc đồ thị hàm số y sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD 2 π /3. Độ dài của cạnh BC bằng A.
2
2
B.
1
2
C. 1 D.
3
2
Đọc tiếp
Cho hai điểm A, B thuộc đồ thị hàm số y = sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD = 2 π /3. Độ dài của cạnh BC bằng
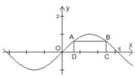
A. 2 2
B. 1 2
C. 1
D. 3 2
Cho (H) là hình phẳng giới hạn bởi parabol
y
3
x
2
và nửa đường tròn có phương trình
y
4
-
x
2
với
-
2
≤
x
≤
2
(phần tô đậm trong hình vẽ). Diện tích của (H) bằng A.
2
π
+
5...
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 x 2 và nửa đường tròn có phương trình y = 4 - x 2 với - 2 ≤ x ≤ 2 (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
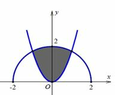
A. 2 π + 5 3 3
B. 4 π + 5 3 3
C. 4 π + 3 3
D. 2 π + 3 3
Cho
(
H
)
là hình phẳng giới hạn bởi parabol
y
3
x
2
và nửa đường tròn có phương trình
y
4
-
x
2
(với
-
2
≤
x
≤
2
) (phần tô đậm trong hình vẽ). Diện tích của
(
H
)
bằng A. ...
Đọc tiếp
Cho ( H ) là hình phẳng giới hạn bởi parabol y = 3 x 2 và nửa đường tròn có phương trình y = 4 - x 2 (với - 2 ≤ x ≤ 2 ) (phần tô đậm trong hình vẽ). Diện tích của ( H ) bằng
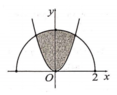
A. 2 π + 3 3
B. 4 π + 5 3 3
C. 2 π + 5 3 3
D. 4 π + 3 3
Cho đồ thị hàm số y1 + cosx (C) và y1 + cos(x-α) (C) trên đoạn
[
0
;
π
]
với
0
α
π
2
. Tính α biết rằng diện tích hình phẳng giới hạn bởi (C) và (C) và đường x 0 thì bằng diện tích hình phẳng giới hạn với(C) và đường y 1, x
π
. Ta được kết quả nào sau đây A.
α
π
6
B.
α...
Đọc tiếp
Cho đồ thị hàm số y=1 + cosx (C) và y=1 + cos(x-α) (C') trên đoạn [ 0 ; π ] với 0 < α < π 2 . Tính α biết rằng diện tích hình phẳng giới hạn bởi (C) và (C') và đường x = 0 thì bằng diện tích hình phẳng giới hạn với(C') và đường y = 1, x = π . Ta được kết quả nào sau đây
A. α = π 6
B. α = π 4
C. α = π 3
D. α = π 12
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0;π/4] thỏa mãn
f
π
4
3
,
∫
0
π
4
f
x
cos
x
d
x
1
và
∫
0
π
4...
Đọc tiếp
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0;π/4] thỏa mãn f π 4 = 3 , ∫ 0 π 4 f x cos x d x = 1 và ∫ 0 π 4 sin x . tan x . f x d x = 2 Tích phân ∫ 0 π 4 sin x f ' x d x bằng
A. 4.
B. 2 + 3 2 2
C. 1 + 3 2 2
D. 6.
Cho (H) là hình phẳng giới hạn bởi parabol
y
2
x
2
4
đường cong
y
1
-
x
2
4
(với
0
≤
x
≤
2
) và trục hoành (tham khảo hình vẽ bên).Diện tích của (H) bằng A. ...
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi parabol y = 2 x 2 4 đường cong y = 1 - x 2 4 (với 0 ≤ x ≤ 2 ) và trục hoành (tham khảo hình vẽ bên).
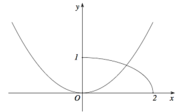
Diện tích của (H) bằng
A. 3 π - 2 12
B. 3 π + 4 2 - 6 12
C. 4 π + 3 2 - 8 12
D. π + 2 - 2 3




