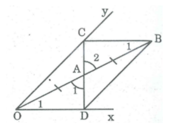
Xét ∆ OAD và ∆ BAC, ta có:
OA = AB (tính chất đối xứng tâm)
∠ A 1 = ∠ A 2 (đối đỉnh)
∠ O 1 = ∠ B 1 (so le trong)
Do đó: ∆ OAD = ∆ BAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua A.

Xét ∆ OAD và ∆ BAC, ta có:
OA = AB (tính chất đối xứng tâm)
∠ A 1 = ∠ A 2 (đối đỉnh)
∠ O 1 = ∠ B 1 (so le trong)
Do đó: ∆ OAD = ∆ BAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua A.
Cho góc xOy và điểm A nằm trong góc đó. Vẽ điểm B đối xứng với O qua A. Qua B vẽ
đường thẳng song song với Ox, cắt Oy ở C. Gọi D là giao điểm của CA và Ox. Chứng minh
rằng các điểm C và D đối xứng với nhau qua điểm A.
Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, gọi C là điểm đối xứng với A qua Oy. Chứng minh rằng điểm B đối xứng với điểm C qua O.
Cho góc vuông xOy điểm A nằm trong góc đó Gọi B là điểm đối xứng với A qua OX Gọi C là điểm đối xứng với A qua Oy Chứng minh rằng điểm B đối xứng với điểm C qua O
Cho góc xOy, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy. Chứng minh rằng OB = OC
góc XOY vuông góc tại O, điểm A nằm trong góc xOy, B là điểm đối xứng với A qua Ox, C là điểm đối xứng của A qua Oy, Gọi D và E lần lượt giao điểm của AB, AC với Ox, Oy
a. Vẽ hình, ghi GT, KL
b. Tứ giác OADE là hình gì, vì sao?
Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, C là điểm đối xứng với A qua Oy. Chứng minh B đối xứng với C qua O.
Cho góc xOy. Điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy. Tính số đo góc xOy để B đối xứng với C qua O.
Cho góc xOy, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy. Tính số đo góc xOy để B đối xứng với C qua O
Cho góc xOy, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với với điểm A qua Ox, điểm C đối xứng với điểm A qua Oy
a) Chứng minh OB=OC
b) Tính số đo góc xOy để B đối xứng với C qua O