Question

Cho góc vuông xOy, điểm A thuộc tia Oy sao cho OA = 2cm. Lấy B là một điểm bất kì thuộc tia Ox. Gọi C là trung điểm của AB. Khi điểm B di chuyển trên tia Ox thì điểm C di chuyển trên đường nào?

Answer 1

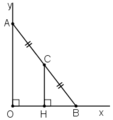
- Cách 1:

Kẻ CH ⊥ Ox.

Ta có CB = CA (gt).

CH // AO (cùng vuông góc Ox)

⇒ HB = OH

⇒ CH là đường trung bình của tam giác AOB

⇒ CH = AO/2 = 1cm.

Điểm C cách tia Ox cố định một khoảng không đổi 1cm nên C di chuyển trên tia song song với Ox, cách Ox một khoảng bằng 1cm và nằm trong góc xOy.

- Cách 2:

Vì C là trung điểm của AB nên OC là trung tuyến ứng với cạnh huyền AB do đó OC = CA.

Điểm C di chuyển trên tia Em thuộc đường trung trực của OA.

Answer 2

m:

Kẻ CH vuông góc với Ox

Ta có: CB = CA (gt) và CH // AO (cùng vuông góc với Ox)

⇒ CH = 12AO = 12.2 = 1 (cm)

Điểm C cách tia Ox cố định một khoảng không đổi 1cm nên điểm C di chuyển trên đường thẳng m song song với Ox và cách Ox một khoảng