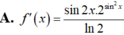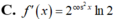Các câu hỏi tương tự
Cho f(x)
log
5
(
sin
x
)
,
x
∈
(
0
;
π
/
2
)
. Tính f(x)
Đọc tiếp
Cho f(x)= log 5 ( sin x ) , x ∈ ( 0 ; π / 2 ) . Tính f'(x)
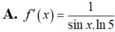
![]()
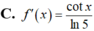
![]()
Cho hàm số yf(x) liên tục trên R thỏa mãn f(1)1 và
∫
0
1
f
(
x
)
d
x
1
3
. Tính tích phân
∫
0
π
2
sin
2
x
.
f
(
sin
x
)
d
x
. A. ...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R thỏa mãn f(1)=1 và ∫ 0 1 f ( x ) d x = 1 3 . Tính tích phân ∫ 0 π 2 sin 2 x . f ' ( sin x ) d x .
A. I = 4 3 .
B. I = 8 3 .
C. I = - 4 3 .
D. I = - 8 3 .
Biết F(x) là một nguyên hàm của hàm số f(x) sin x và đồ thị hàm số y F(x) đi qua điểm M(0;1) . Tính
F
π
2
. A.
F
π
2
0
B.
F
π
2
1
C.
F
π
2
2
D.
F...
Đọc tiếp
Biết F(x) là một nguyên hàm của hàm số f(x) = sin x và đồ thị hàm số y = F(x) đi qua điểm M(0;1) . Tính F π 2 .
A. F π 2 = 0
B. F π 2 = 1
C. F π 2 = 2
D. F π 2 = - 1
Biết F(x) là một nguyên hàm của hàm f(x) sin 2x và
F
π
4
1
.Tính
F
π
6
A.
F
π
6
5
4
B.
F
π
6
0
C.
F
π
6...
Đọc tiếp
Biết F(x) là một nguyên hàm của hàm f(x) = sin 2x và F π 4 = 1 .Tính F π 6
A. F π 6 = 5 4
B. F π 6 = 0
C. F π 6 = 3 4
D. F π 6 = 1 2
Cho hàm số
y
f
(
x
)
thỏa mãn
f
(
2
)
1
4
và
f
(
x
)
2
x
.
[
f
(
x
)
]
2
với
∀
x
∈
R
tính...
Đọc tiếp
Cho hàm số y = f ( x ) thỏa mãn f ( 2 ) = 1 4 và f ' ( x ) = 2 x . [ f ( x ) ] 2 với ∀ x ∈ R tính f ( 1 )
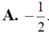
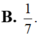
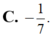
![]()
Cho hàm số yf(x). Hàm số f(x) có biến thiên Bất phương trình f(sin x) -3x + m đúng với mọi
x
∈
-
π
2
;
π
2
khi và chỉ khi A.
m
≥
f
(
1
)
+
3
π...
Đọc tiếp
Cho hàm số y=f(x). Hàm số f'(x) có biến thiên
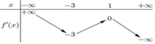
Bất phương trình f(sin x)< -3x + m đúng với mọi x ∈ - π 2 ; π 2 khi và chỉ khi
A. m ≥ f ( 1 ) + 3 π 2
B. m > f ( - 1 ) - 3 π 2
C. m > f ( π 2 ) + 3 π 2
D. m > f ( 1 ) + 3 π 2
Cho hàm số f(x) có f(x) và f(x) liên tục trên
ℝ
. Biết f(2)4 và f(-1) -2. Tính
∫
-
1
2
f
(
x
)
d
x
A. -8. B. -6. C. 2. D. 6.
Đọc tiếp
Cho hàm số f(x) có f'(x) và f"(x) liên tục trên ℝ . Biết f'(2)=4 và f'(-1)= -2. Tính ∫ - 1 2 f " ( x ) d x
A. -8.
B. -6.
C. 2.
D. 6.
Cho f(x)
log
3
x
x
-
2
;
x
∈
(
2
;
+
∞
)
. Tính f(x)
Đọc tiếp
Cho f(x) = log 3 x x - 2 ; x ∈ ( 2 ; + ∞ ) . Tính f'(x)
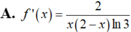
![]()
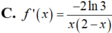
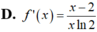
Cho hàm số yf(x) liên tục trên
ℝ
và có đồ thị như hình bên. Phương trình f( 2 sin x) m có đúng ba nghiệm phân biệt thuộc đoạn
-
π
;
π
khi và chỉ khi A.
m
∈
-
3
;
1
B.
m
∈
-...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình bên. Phương trình f( 2 sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn - π ; π khi và chỉ khi
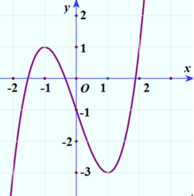
A. m ∈ - 3 ; 1
B. m ∈ - 3 ; 1
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]
Cho f(x) = \(\dfrac{1}{x-1}\) thỏa F(0)=2, F(2)=3. Tính F(3)+F(-3)