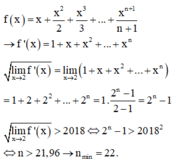Các câu hỏi tương tự
Cho hàm số y f(x) có đạo hàm
f
x
x
x
+
1
x
-
2
2
với mọi
x
∈
ℝ
. Giá trị nhỏ nhất của hàm số y f(x) trên đoạn [-1 ;2] là A. f(-1) B. f(0) C. f(3) D. f(2)
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f ' x = x x + 1 x - 2 2 với mọi x ∈ ℝ . Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [-1 ;2] là
A. f(-1)
B. f(0)
C. f(3)
D. f(2)
Cho hàm số f(x) liên tục trên
ℝ
+
thỏa mãn
f
x
≥
x
+
1
x
,
∀
x
∈
ℝ
+
và f(1) 1. Tính giá trị nhỏ nhất của f(2). A. 3 B. 2 C.
5
2
+
ln
2
D. 4
Đọc tiếp
Cho hàm số f(x) liên tục trên ℝ + thỏa mãn f ' x ≥ x + 1 x , ∀ x ∈ ℝ + và f(1) = 1. Tính giá trị nhỏ nhất của f(2).
A. 3
B. 2
C. 5 2 + ln 2
D. 4
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
x
+
1
x
-
2
2
với mọi
x
∈
ℝ
. Giá trị nhỏ nhất của hàm số yf(x) trên đoạn [-1;2] là A.
f
(
-
1
)
B.
f...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x x + 1 x - 2 2 với mọi x ∈ ℝ . Giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [-1;2] là
A. f ( - 1 )
B. f ( 0 )
C. f ( 3 )
D. f ( 2 )
Cho hàm số
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
,
(
a
,
b
,
c
,
d
∈
ℝ
)
thỏa mãn
a
0
,
d
0
2018
,
a
+...
Đọc tiếp
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d , ( a , b , c , d ∈ ℝ ) thỏa mãn a > 0 , d > 0 > 2018 , a + b + c + d - 2018 < 0 Tìm số điểm cực trị của hàm số y = f ( x ) - 2018
A. 2
B. 1
C. 3
D. 5
Cho hàm số
y
f
x
a
x
3
+
b
x
3
+
c
x
+
d
a
,
b
,
c
,
d
∈
ℝ
;
a
≠...
Đọc tiếp
Cho hàm số y = f x = a x 3 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a ≠ 0 biết f'(-1)=3. Tính lim ∆ x → ∞ f 1 + ∆ x + f 1 ∆ x
A. 3
B. -3
C. 1
D. -1
Cho hàm số
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
với
a
,
b
,
c
,
d
∈
ℝ
,
a
0
và
d
2018
a
+
b
+...
Đọc tiếp
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d với a , b , c , d ∈ ℝ , a > 0 và d > 2018 a + b + c + d - 2018 < 0 . Số cực trị của hàm số y = f ( x ) - 2018 bằng
A. 3
B. 2
C. 1
D. 5
Cho hàm số f(x) thỏa mãn f(1) 1/3 và
f
x
x
f
x
2
với mọi x ϵ ℝ. Giá trị f(2) bằng A. 16/3 B. 3/16 C. 2/3 D. 3/2
Đọc tiếp
Cho hàm số f(x) thỏa mãn f(1) = 1/3 và f ' x = x f x 2 với mọi x ϵ ℝ. Giá trị f(2) bằng
A. 16/3
B. 3/16
C. 2/3
D. 3/2
Cho hàm số f(x) liên tục trên
ℝ
và
∀
x
∈
0
;
2018
, ta có
f
(
x
)
0
và
f
(
x
)
.
f
(
2018
−
x
)
1
. Giá trị của tích phân
I
∫
0
2018...
Đọc tiếp
Cho hàm số f(x) liên tục trên ℝ và ∀ x ∈ 0 ; 2018 , ta có f ( x ) > 0 và f ( x ) . f ( 2018 − x ) = 1 . Giá trị của tích phân I = ∫ 0 2018 1 1 + f ( x ) d x là
A. 2018
B. 0
C. 1009
D. 4016
Cho hàm số
y
f
x
có đạo hàm
f
x
x
x
+
1
x
-
2
2
với mọi
x
∈
ℝ
. Giá trị nhỏ nhất của hàm số
y
f
x
trên đoạn...
Đọc tiếp
Cho hàm số y = f x có đạo hàm f ' x = x x + 1 x - 2 2 với mọi x ∈ ℝ . Giá trị nhỏ nhất của hàm số y = f x trên đoạn - 1 ; 2 là
A. f - 1
B. f 0
C. f 3
D. f 2