Các câu hỏi tương tự
Cho hàm số f (x) có đạo hàm cấp 3 xác định và liên tục trên R thoả mãn f(x)f‴(x)
x
(
x
2
-
1
)
(
x
-
4
)
,
∀
x
∈
R
. Hàm số
g
(
x
)
(
f
(
x
)
)
2
-
2
f...
Đọc tiếp
Cho hàm số f (x) có đạo hàm cấp 3 xác định và liên tục trên R thoả mãn f(x)f‴(x) = x ( x 2 - 1 ) ( x - 4 ) , ∀ x ∈ R . Hàm số g ( x ) = ( f ' ( x ) ) 2 - 2 f ( x ) f '' ( x ) đồng biến trên khoảng nào ?
A. (0;1).
B. (-1;0).
C. ( 4 ; + ∞ ) .
D. ( - ∞ ; - 1 ) .
Cho hàm số yf(x) có đạo hàm liên tục trên R và có đồ thị hàm số yf (x) như hình vẽ bên. Xét hàm số g(x)f(x^2-3) và các mệnh đề sau:1. Hàm số g(x) có 3 điểm cực trị.2. Hàm số g(x)đạt cực tiểu tại x 0.3. Hàm số g(x)đạt cực đại tại x 2.4. Hàm số g(x)đồng biến trên khoảng (-2;0).5. Hàm số g(x)nghịch biến trên khoảng (-1;1). Có bao nhiêu mệnh đề đúng trong các mệnh đề trên? A. 1. B. 4. C. 3. D. 2.
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Cho hàm số yf(x) và yg(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị các hàm số yf(x) , yg(x) và hai đường thẳng x a, x b(a b) Diện tích của D được tính theo công thức A.
S
∫
a
b
f
x
-
g
x
d
x
B. ...
Đọc tiếp
Cho hàm số y=f(x) và y=g(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị các hàm số y=f(x) , y=g(x) và hai đường thẳng x= a, x= b(a < b) Diện tích của D được tính theo công thức
A. S = ∫ a b f x - g x d x
B. S = ∫ a b f x - g x d x
C. ∫ a b f x d x - ∫ a b g x d x
D. S = ∫ b a f x - g x d x
Cho hàm số yf(x) nhận giá trị không âm và liên tục trên đoạn [0;1]. Đặt
g
(
x
)
1
+
2
∫
0
x
f
(
t
)
d
t
. Biết
g
(
x
)
≥
[
f
(
x
)
]
3
với mọi
x
∈
[
0
;...
Đọc tiếp
Cho hàm số y=f(x) nhận giá trị không âm và liên tục trên đoạn [0;1]. Đặt g ( x ) = 1 + 2 ∫ 0 x f ( t ) d t . Biết g ( x ) ≥ [ f ( x ) ] 3 với mọi x ∈ [ 0 ; 1 ] . Tích phân ∫ 0 1 [ g ( x ) ] 2 3 d x có giá trị lớn nhất bằng
A. 5 3
B. 4.
C. 4 3
D. 5.
Cho hàm số
y
f
(
x
)
,
y
g
(
x
)
liên tục trên đoạn
[
a
;
b
]
(
a
b
)
. Hình phẳng D giới hạn bởi đồ thị hai hàm số
y
f
(
x
)
,
y
g
(
x
)
và hai đường thẳng x a, x b có diệ...
Đọc tiếp
Cho hàm số y = f ( x ) , y = g ( x ) liên tục trên đoạn [ a ; b ] ( a < b ) . Hình phẳng D giới hạn bởi đồ thị hai hàm số y = f ( x ) , y = g ( x ) và hai đường thẳng x = a, x= b có diện tích là
A. S D = ∫ a b f ( x ) − g ( x ) d x .
B. S D = ∫ a b f ( x ) − g ( x ) d x .
C. S D = π ∫ a b f ( x ) − g ( x ) d x .
D. S D = ∫ b a f ( x ) − g ( x ) d x .
Hàm số y f(x) có đồ thị y f(x) như hình vẽ.Xét hàm số:
g
(
x
)
f
(
x
)
-
1
3
x
3
-
3
4
x
2
+
3
2
x
+
2017
Trong các mệnh đề dưới đây:(I) g(0) g(1)(II)
m
i...
Đọc tiếp
Hàm số y = f(x) có đồ thị y = f'(x) như hình vẽ.
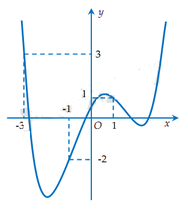
Xét hàm số:
g ( x ) = f ( x ) - 1 3 x 3 - 3 4 x 2 + 3 2 x + 2017
Trong các mệnh đề dưới đây:
(I) g(0) < g(1)
(II) m i n x ∈ - 3 ; 1 g ( x ) = g ( - 1 )
(III) Hàm số g(x) nghịch biến trên (-3;-1)
(IV) m a x x ∈ - 3 ; 1 g ( x ) = m a x g ( - 3 ) , g ( 1 )
Số mệnh đề đúng là:
A. 2
B. 1
C. 3
D. 4
Cho hàm số yf(x) liên tục trên R có đạo hàm cấp 3 với f’’’(x)0 và thỏa mãn
f
(
x
)
2018
1
-
f
(
x
)
2
x
(...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R có đạo hàm cấp 3 với f’’’(x)=0 và thỏa mãn f ( x ) ' 2018 1 - f ' ' ( x ) = 2 x ( x + 1 ) 2 ( x - 2018 ) 2019 : f ' ' ( x ) , ∀ x ∈ R Hàm số g ( x ) = f ' ( x ) 2019 1 - f ' ' ( x ) có bao nhiêu điểm cực trị?
A. 1
B.2
C.3
D. 4
Cho hàm số
f
x
a
x
+
b
c
x
+
d
với
a
,
b
,
c
,
d
∈
R
có đồ thị hàm số yf(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số yf(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng. A. 2 B. 5 C. 4...
Đọc tiếp
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.

A. 2
B. 5
C. 4
D. 6
Cho hàm số y f(x) có đạo hàm
f
(
x
)
x
(
x
-
1
)
4
(
x
2
+
m
x
+
9
)
với mọi. Có bao nhiêu giá trị nguyên dương của m để hàm số g(x) f(3 - x) đồng biến trên khoảng
3...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f ' ( x ) = x ( x - 1 ) 4 ( x 2 + m x + 9 ) với mọi. Có bao nhiêu giá trị nguyên dương của m để hàm số g(x) = f(3 - x) đồng biến trên khoảng 3 ; + ∞
A. 5
B. 6
C. 7
D. Vô số
Cho hàm số
y
f
x
a
x
3
+
b
x
3
+
c
x
+
d
a
,
b
,
c
,
d
∈
ℝ
;
a
≠...
Đọc tiếp
Cho hàm số y = f x = a x 3 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a ≠ 0 biết f'(-1)=3. Tính lim ∆ x → ∞ f 1 + ∆ x + f 1 ∆ x
A. 3
B. -3
C. 1
D. -1