Cho đường tròn tâm O đường kính AB. Gọi d và d' là các tiếp tuyến tại A và B. Lấy C bất kì thuộc d, đường thẳng vuông góc với OC tại O cắt d' tại D. AD cắt BC tại N.
a, Chứng minh CD là tiếp tuyến của (O) tại tiếp điểm M
b, Tìm vị trí C trên d sao cho (AC + BD) đạt giá trị nhỏ nhất
c, Biết AB = 4a, tính giá trị của AC.BD và 1 O C 2 + 1 O D 2 theo a
d, Chứng minh MN vuông góc với AB và N là trung điểm của MH với H là giao điểm của MN và AB
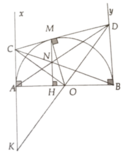
a, Kẻ OM ⊥ CD
Gọi K = OD ∩ d => ∆COK = ∆COD
=> OK = OD => OM = OA = R => CD là tiếp tuyến
b, AC+BD=CM+DM=CD ≥ AB
Do đó min (AC+BD)=AB
<=> CD//AB => ABCD là hình chữ nhật <=> AC = AO
c, AC.BD = MC.MD = O M 2 = 4 a 2
=> 1 O C 2 + 1 O D 2 = 1 4 a 2
d, Từ tính chất hai giao tuyến => MN//BD => MNAB hay MHAB;
AC//BD; MN//BD; NH//BD
=> M N B D = N H B D => MN = NH












