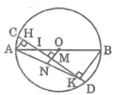
Kẻ OM ⊥ CD cắt AD tại N
Ta có: MC = MD (đường kính dây cung)
Hay MH + CH = MK + KD (1)
Ta có: OM // BK (cùng vuông góc với CD)
Hay: MN // BK
Mà: OA = OB (= R)
Suy ra: NA = NK (tính chất đường trung bình của tam giác)
Lại có: OM // AH (cùng vuông góc với CD)
Hay: MN // AH
Mà: NA = NK (chứng minh trên)
Suy ra: MH = MK (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: CH = DK
Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB, Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK.
Gợi ý: Kẻ OM vuông góc với CD
Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB, Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK.
Gợi ý: Kẻ OM vuông góc với CD.
Cho (O) đường kính AB, dây CD cắt đường kính AB tại I. Gọi , K lần lượt theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh CH= DK
Cho đường tròn tâm O đường kính AB. Dây CD ko cắt đường kính AB. Gọi H và K theo thứ tự là chân đường vuông góc kẻ từ A và B đến CD. CMR CH = BK
Cho đường tròn O đường kính AB, dây CD ko cắt đường kính AB, Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B dến CD. Chứng minh rằng CH= DK
Giúp mình với ngày kia phải thi nên cần câu trả lời gấp
Cho nửa đường tròn tâm O đường kính AB, dây CD. Gọi H, K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD.
b) Chứng minh SAHKB=SABC + SDBA
Giải gấp giúp em với ạ.
Cho đường tròn tâm O có đường kính AB. Dây CD không cắt đường kính AB. Gọi H và K là chân đường vuông góc kẻ từ A và B xuống DC. CM: CH =DK.
Cho ∆MAB có 3 góc nhọn. Vẽ đường tròn tâm O đường kính AB cắt MA và MB lần lượt tại D và C. Gọi H là giao điểm của AC và BD. a) Chứng minh: ∆ ABC vuông và MH ⊥ AB b) Gọi P, N, Q theo thứ tự là chân các đường vuông góc kẻ từ A, O, B đến CD. Chứng minh: PD = CQ c) Gọi I là trung điểm của MH. Chứng minh: IC là tiếp tuyến của (O
Cho nửa đường tròn tâm O đường kính AB, kẻ dây CD bất kỳ không trùng với AB. Gọi B, K theo thứ tự là chân đường vuông góc kẻ từ A và B đến đường thẳng CD.
a/ Chứng minh CH = DK
b/ Chứng minh SABCD = SACB + SADB
c/ Tìm vị tri dây CD để diện tích tứ giác AHKB lớn nhất, tính diện tích lớn nhất đó biết AB = 30 cm, CD = 18 cm.
