Các câu hỏi tương tự
Cho đường tròn (O;R) đường kính AB. Gọi H là một điểm bất kỳ trên đoạn OA (H khác hai điểm O, A). Dựng đường thẳng d vuông góc với OA tại H. Trên d lấy điểm C ở ngoài đường tròn (O). Kẻ các tiếp tuyến CM, CN với đường tròn (O); M và N là tiếp điểm, M cùng phía với A bờ CH. Các đường thẳng CM, CN cắt đường thẳng AB tại P và Q. Đường thẳng qua O và vuông góc với AB cắt MN tại K. CK cắt AB tại I. Chứng minh rằng: 1) HC là tia phân giác của góc MHN 2) I là trung điểm của đoạn thẳng PQ 3) Ba đường th...
Đọc tiếp
Cho đường tròn (O;R) đường kính AB. Gọi H là một điểm bất kỳ trên đoạn OA (H khác hai điểm O, A). Dựng đường thẳng d vuông góc với OA tại H. Trên d lấy điểm C ở ngoài đường tròn (O). Kẻ các tiếp tuyến CM, CN với đường tròn (O); M và N là tiếp điểm, M cùng phía với A bờ CH. Các đường thẳng CM, CN cắt đường thẳng AB tại P và Q. Đường thẳng qua O và vuông góc với AB cắt MN tại K. CK cắt AB tại I. Chứng minh rằng: 1) HC là tia phân giác của góc MHN 2) I là trung điểm của đoạn thẳng PQ 3) Ba đường thẳng PN, QM và CH đồng quy.
Trên nửa đường tròn tâm O đường kính AB với AB = 2022, lấy điểm C (C khác A và B), từ C kẻ CH vuông góc với AB (H thuộc AB). Gọi D là điểm bất kỳ trên đoạn CH (D khác C và H), đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là E. a) Chứng minh tứ giác BHDE là tứ giác nội tiếp; b) Chứng minh: AD.EC=CD.AC; c) Chứng minh: AD.AE+BH.BA=2022^2
Cho đường tròn (O;R), đường kính AB. Trên đoạn thẳng OA lấy điểm M bất kỳ (M không trùng với A và O) Đường thẳng qua M vuông góc với AB cắt đường tròn (O) tại C. Gọi D là điểm chính giữa cung AB (c,D nằm khác phía đới với AB), gợi I là trung điểm của dây cung BC
a. Chứng minh tứ giác MCIO nội tiếp
b. Xác định vị trí điểm M để diện tích tam giác MCD lớn nhất
Cho đường tròn (O; R) có đường kính AB. Bán kính CO vuông góc với AB. M là một điẻm bất kỳ trên cung nhỏ AC (M khác A, C), BM cắt AC tại H. Gọi K là hình chiếu của H trên ABa, Chứng minh CBKH là tứ giác nội tiếpb, Chứng minh:
A
C
M
^
A
C
K
^...
Đọc tiếp
Cho đường tròn (O; R) có đường kính AB. Bán kính CO vuông góc với AB. M là một điẻm bất kỳ trên cung nhỏ AC (M khác A, C), BM cắt AC tại H. Gọi K là hình chiếu của H trên AB
a, Chứng minh CBKH là tứ giác nội tiếp
b, Chứng minh: A C M ^ = A C K ^
c, Trên đoạn thẳng BM lấy điểm E sao cho BE = AM. Chứng minh tam giác ECM là tam giác vuông cân tại C
d, Gọi d là tiếp tuyến của (O) tại điểm A; cho P là điểm nằm trên d ao cho hai điểm P, C nằm trong cùng một nưanr mặt phẳng bờ AB và A P . M B M A = R . Chứng minh đường thẳng PB đi qua trung điểm của đoạn thẳng HK
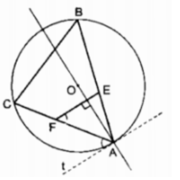
Bài 4(3 điểm). Cho đường tròn (O; R), đường kính AB. Lấy điểm C bất kỳ trên đường tròn (O; R) (C không trùng A; AC BC). Qua C kẻ dây CD của đường tròn (O; R) vuông góc với đường kính AB tại I. Lấy điểm E sao cho I là trung điểm AE. Tia DE cắt đoạn thẳng BC tại F. Gọi K là trung điểm của BE. 1) Chứng minh tam giác BCD cân. 2) Chứng minh AC I/ DE và chứng minh F thuộc đường tròn tâm K đường kính BE. 3) Chứng minh IF là tiếp tuyến của đường tròn tâm K đường kính BE. 4) Lấy điểm M trên đoạn thẳng O...
Đọc tiếp
Bài 4(3 điểm). Cho đường tròn (O; R), đường kính AB. Lấy điểm C bất kỳ trên đường tròn (O; R) (C không trùng A; AC < BC). Qua C kẻ dây CD của đường tròn (O; R) vuông góc với đường kính AB tại I. Lấy điểm E sao cho I là trung điểm AE. Tia DE cắt đoạn thẳng BC tại F. Gọi K là trung điểm của BE. 1) Chứng minh tam giác BCD cân. 2) Chứng minh AC I/ DE và chứng minh F thuộc đường tròn tâm K đường kính BE. 3) Chứng minh IF là tiếp tuyến của đường tròn tâm K đường kính BE. 4) Lấy điểm M trên đoạn thẳng OC sao cho OM = CI. Chứng minh khi điểm C di chuyển trên nửa đường tròn (O; R) không chứa điểm D (C khác A, B) thì điểm M chạy trên một đường tròn cố định.
Cho đường tròn (O;R) đường kính AB cố định. Trên tia đối của tia AB lấy điểm C sao cho ACR. Qua C kẻ đường thẳng d vuông góc với CA. lấy điểm M bất kỳ trên đường tròn (O) không trùng với A, B. Tia BM cắt đường thẳng d tại P. Tia CM cắt đường tròn (O) tại điểm thứ hai là N, tia PA cắt đường tròn (O) tại điểm thứ hai là Q.1. Chứng minh tứ giác ACPM là tứ giác nội tiếp.2. Tính BM.BP theo R.3. Chứng minh hai đường thẳng PC và NQ song song.4. Chứng minh trọng tâm G của tam giác CMB luôn nằm trên mộ...
Đọc tiếp
Cho đường tròn (O;R) đường kính AB cố định. Trên tia đối của tia AB lấy điểm C sao cho AC=R. Qua C kẻ đường thẳng d vuông góc với CA. lấy điểm M bất kỳ trên đường tròn (O) không trùng với A, B. Tia BM cắt đường thẳng d tại P. Tia CM cắt đường tròn (O) tại điểm thứ hai là N, tia PA cắt đường tròn (O) tại điểm thứ hai là Q.
1. Chứng minh tứ giác ACPM là tứ giác nội tiếp.
2. Tính BM.BP theo R.
3. Chứng minh hai đường thẳng PC và NQ song song.
4. Chứng minh trọng tâm G của tam giác CMB luôn nằm trên một đường tròn cố định khi điểm M thay đổi trên đường tròn (O).
làm câu 3 thôi
Cho đường tròn (O;R) và đường thẳng d cố định, sao cho khoảng cách từ tâm O đến đường thẳng d lớn hơn bán kìn R của đường tròn O. Trên đường thẳng d lấy điểm M bất kỳ. Từ M kẻ MC là tiếp tuyến của đường tròn (O;R), C là tiếp điểm. Vẽ CH vuông góc với OM tại H, cắt (O;R) tại B.a) Cho biết vị trí tương đối của đường tròn (O;R) và đường thẳng d? Giải thích vì sao?b) Chứng minh: MB là tiếp tuyến của (O;R)c) Chứng minh rằng: Khi điểm M di chuyển trên đường thẳng d thì đoạn thẳng BC luôn đi qua 1 điể...
Đọc tiếp
Cho đường tròn (O;R) và đường thẳng d cố định, sao cho khoảng cách từ tâm O đến đường thẳng d lớn hơn bán kìn R của đường tròn O. Trên đường thẳng d lấy điểm M bất kỳ. Từ M kẻ MC là tiếp tuyến của đường tròn (O;R), C là tiếp điểm. Vẽ CH vuông góc với OM tại H, cắt (O;R) tại B.
a) Cho biết vị trí tương đối của đường tròn (O;R) và đường thẳng d? Giải thích vì sao?
b) Chứng minh: MB là tiếp tuyến của (O;R)
c) Chứng minh rằng: Khi điểm M di chuyển trên đường thẳng d thì đoạn thẳng BC luôn đi qua 1 điểm cố định.
Cho đường tròn (O; R) và đường thẳng xy không có điểm chung với đường tròn. Lấy một điểm A bất kỳ thuộc xy. Từ A kẻ tiếp tuyến AB với đường tròn (O) (B là tiếp điểm). Ọua B kẻ đường thẳng vuông góc với AO, cát AO tại K và cắt đường tròn (O) tại điểm thứ hai là c.a) Tính độ dài OK nếu R 5cm, OA 10 cm.b) Chứng minh ràng: AC là tiếp tuyến của đường tròn (O).c) Kẻ OH vuông góc với xy tại H, BC cắt OH tại I. Chứng minh rằng: Khi A di chuyển trên đường thẳng xy thì độ dài đoạn thẳng OI không đổi....
Đọc tiếp
Cho đường tròn (O; R) và đường thẳng xy không có điểm chung với đường tròn. Lấy một điểm A bất kỳ thuộc xy. Từ A kẻ tiếp tuyến AB với đường tròn (O) (B là tiếp điểm). Ọua B kẻ đường thẳng vuông góc với AO, cát AO tại K và cắt đường tròn (O) tại điểm thứ hai là c.
a) Tính độ dài OK nếu R = 5cm, OA = 10 cm.
b) Chứng minh ràng: AC là tiếp tuyến của đường tròn (O).
c) Kẻ OH vuông góc với xy tại H, BC cắt OH tại I. Chứng minh rằng: Khi A di chuyển trên đường thẳng xy thì độ dài đoạn thẳng OI không đổi.
Cho nữa đường tròn (O;R) đường kính AB. Một điểm M cố định thuộc đoạn thẳng OB (M khác B và M khác O). Đường thẳng d vuông góc với AB tại M cắt nữa đường tròn đã cho tại N. Trên cúng NB lấy điểm E bất kì ( E khác B và E khác N). Tia BE cắt đường thẳng d tại C, đường thẳng AC cắt nữa đường tròn tại D. Gọi giao điểm của AE với d là HGọi K là tâm đường tròn ngoại tiếp tam giác AHC. Chứng minh rằng khi E di động trên cung NB thì K luôn nằm trên 1 đường thẳng cố định
Đọc tiếp
Cho nữa đường tròn (O;R) đường kính AB. Một điểm M cố định thuộc đoạn thẳng OB (M khác B và M khác O). Đường thẳng d vuông góc với AB tại M cắt nữa đường tròn đã cho tại N. Trên cúng NB lấy điểm E bất kì ( E khác B và E khác N). Tia BE cắt đường thẳng d tại C, đường thẳng AC cắt nữa đường tròn tại D. Gọi giao điểm của AE với d là H
Gọi K là tâm đường tròn ngoại tiếp tam giác AHC. Chứng minh rằng khi E di động trên cung NB thì K luôn nằm trên 1 đường thẳng cố định