Các câu hỏi tương tự
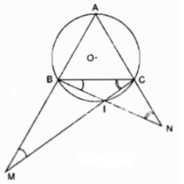
Cho đường tròn tâm O bán kính R. Lấy 3 điểm A, B, C trên đường tròn đó sao cho AB = BC = CA. Gọi I là điểm bất kỳ của cung nhỏ BC (và I không trùng với B, C). Gọi M là giao điểm của CI và AB. Gọi N là giao điểm của BI và AC. Chứng minh: ∠ ANB = ∠ BCI
Cho đường tròn tâm O bán kính R và dây AB bất kỳ. Gọi M là điểm chính giữa của cung nhỏ AB. E và F là hai điểm bất kỳ trên dây AB. Gọi C và D tương ứng là giao điểm của ME, MF của đường tròn (O). Chứng minh ∠ EFD + ∠ ECD = 180 °
Cho đường tròn O đường kính AB 2R . Lấy điểm C trên đường tròn O sao cho ACR và lấy điểm M bất kỳ trên cung nhỏ BC ( M ko trùng với B và C) . Gọi H là giao điểm của AM và BC . Đường thẳng AC cắt đường thẳng BM tại D1, Cmr 4 điểm C,D,M,H cùng thuộc 1 đường tròn2, DH cắt AB tại K .Cmr DK vuông góc với AB3, Cmr CKMCOM và tâm đường tròn ngoại tiếp tam giác CKM nằm trên đường trung trực của OC
Đọc tiếp
Cho đường tròn O đường kính AB =2R . Lấy điểm C trên đường tròn O sao cho AC=R và lấy điểm M bất kỳ trên cung nhỏ BC ( M ko trùng với B và C) . Gọi H là giao điểm của AM và BC . Đường thẳng AC cắt đường thẳng BM tại D
1, Cmr 4 điểm C,D,M,H cùng thuộc 1 đường tròn
2, DH cắt AB tại K .Cmr DK vuông góc với AB
3, Cmr CKM=COM và tâm đường tròn ngoại tiếp tam giác CKM nằm trên đường trung trực của OC
Cho đường tròn O đường kính AB 2R . Lấy điểm C trên đường tròn O sao cho ACR và lấy điểm M bất kỳ trên cung nhỏ BC ( M ko trùng với B và C) . Gọi H là giao điểm của AM và BC . Đường thẳng AC cắt đường thẳng BM tại D1, Cmr 4 điểm C,D,M,H cùng thuộc 1 đường tròn2, DH cắt AB tại K .Cmr DK vuông góc với AB3, Cmr CKMCOM và tâm đường tròn ngoại tiếp tam giác CKM nằm trên đường trung trực của OC
Đọc tiếp
Cho đường tròn O đường kính AB =2R . Lấy điểm C trên đường tròn O sao cho AC=R và lấy điểm M bất kỳ trên cung nhỏ BC ( M ko trùng với B và C) . Gọi H là giao điểm của AM và BC . Đường thẳng AC cắt đường thẳng BM tại D
1, Cmr 4 điểm C,D,M,H cùng thuộc 1 đường tròn
2, DH cắt AB tại K .Cmr DK vuông góc với AB
3, Cmr CKM=COM và tâm đường tròn ngoại tiếp tam giác CKM nằm trên đường trung trực của OC
Cho tam giác ABC nhọn (AB AC) nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC. Gọi M là trung điểm của BCc) Gọi N là giao điểm của AH với đường tròn (O) (N khác A). Gọi D là điểm bất kì trên cung nhỏ NC của đường tròn tâm (O) (D khác N và C). Gọi E là điểm đối xứng với D qua AC, K là giao điểm của AC và HE. Chứng minh rằng ACH ADK.
Đọc tiếp
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC. Gọi M là trung điểm của BC
c) Gọi N là giao điểm của AH với đường tròn (O) (N khác A). Gọi D là điểm bất kì trên cung nhỏ NC của đường tròn tâm (O) (D khác N và C). Gọi E là điểm đối xứng với D qua AC, K là giao điểm của AC và HE. Chứng minh rằng ACH = ADK.
Cho (O) có AB là đường kính.Lấy điểm C trên (O) và lấy điểm M bất kì trên cung nhỏ BC(M không trùng B,C).Gọi H là giao điểm của AM và BC,D là giao điểm của AC và BM
a)Chứng minh bốn điểm C,D,M,H cùng thuộc một đường tròn(phần này không cần làm ạ)
b)Cho DH cắt AB tại K.Chứng minh rằng góc CKM=góc COM và tâm của đường tròn ngoại tiếp ΔCKM nằm trên đường trung trức của OC
cho đường tròn tâm (O) , có đường kính AB 2R , lấy 1 điểm C ( C thuộc đường tròn ) sao cho AC R và lấy điểm D bất kì trên cung nhỏ BC ( D không trùng điểm B và C ) . Gọi E là giao điểm của AD và BC . đường thẳng đi qua E vuông góc với AB tại H cắt AC tại F . M là trung điêm của EFa/ CM : HA.HB HE.HFb/ CM : CM là tiếp tuyến của đường tròn tâm (O)c/ Xác định vị trí của D để chu vi của tứ giác ABCD lớn nhất
Đọc tiếp
cho đường tròn tâm (O) , có đường kính AB = 2R , lấy 1 điểm C ( C thuộc đường tròn ) sao cho AC = R và lấy điểm D bất kì trên cung nhỏ BC ( D không trùng điểm B và C ) . Gọi E là giao điểm của AD và BC . đường thẳng đi qua E vuông góc với AB tại H cắt AC tại F . M là trung điêm của EF
a/ CM : HA.HB = HE.HF
b/ CM : CM là tiếp tuyến của đường tròn tâm (O)
c/ Xác định vị trí của D để chu vi của tứ giác ABCD lớn nhất
Cho đường tròn tâm O bán kính R và hai dây AB, CD bất kì. Gọi M là điểm chính giữa của cung nhỏ AB. Gọi E và F tương ứng là giao điểm của MC, MD với dây AB. Gọi I và J tương ứng là giao điểm của DE, CF với đường tròn (O). Chứng minh IJ song song với AB.
Cho đường tròn (O;R) và A nằm ngoài đường tròn,Kẻ các tiếp tuyến AB;AC với đường tròna)Chứng minh ABOC nội tiếpb)Gọi E là giao điểm của BC và OA.Chứng minh BE vuông góc OA và OE.OAR^2c)Trên cung nhỏ BC của (O) lấy K bất kì sao cho K không trùng với B và C.Tiếp tuyến tại K của đường tròn (O) cắt AB,AC theo thứ tự tại P và Q. Chứng minh tam giác APQ có chu vi không đổi khi K di chuyển trên cung nhỏ BC d).Đường thẳng đi qua O và vuông góc với OA cắt AB,AC theo thứ tự tại các điểm M và N. chứng minh...
Đọc tiếp
Cho đường tròn (O;R) và A nằm ngoài đường tròn,Kẻ các tiếp tuyến AB;AC với đường tròn
a)Chứng minh ABOC nội tiếp
b)Gọi E là giao điểm của BC và OA.Chứng minh BE vuông góc OA và OE.OA=R^2
c)Trên cung nhỏ BC của (O) lấy K bất kì sao cho K không trùng với B và C.Tiếp tuyến tại K của đường tròn (O) cắt AB,AC theo thứ tự tại P và Q. Chứng minh tam giác APQ có chu vi không đổi khi K di chuyển trên cung nhỏ BC
d).Đường thẳng đi qua O và vuông góc với OA cắt AB,AC theo thứ tự tại các điểm M và N. chứng minh tam giác PMO đồng dạng tam giác ONQ