Question

Cho đường tròn (O;R =5cm). Từ điểm M ngoài đường tròn vẽ các tiếp tuyến MA,MB (A;B là tiếp tuyến). Đường thẳng AB cắt OM tại H. Cho OM =10cm. Tính diện tích △ABM?

Answer 1

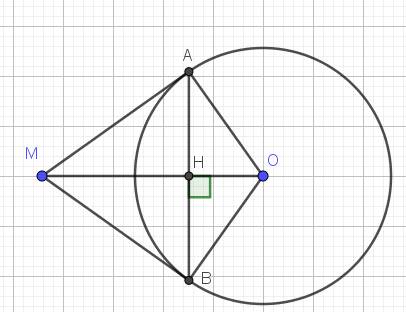
Lời giải:

$MA,MB$ là tiếp tuyến $(O)$ nên $MA\perp OA, MB\perp OB$
Áp dụng định lý Pitago:

$MA^2=MO^2-OA^2=10^2-5^2=75$

Áp dụng công thức hệ thức lượng trong tam giác vuông $MAO$, đường cao $AH$ ta có:

$MA^2=MH.MO\Rightarrow MH=\frac{MA^2}{MO}=\frac{75}{10}=7,5$ (cm)

$HO=MO-MH=10-7,5=2,5$ (cm)

$AH^2=MH.HO=7,5.2,5=18,75$

$\Rightarrow AH=\sqrt{18,75}=4,33$ (cm)

$OA=OB; MA=MB$ (theo tính chất 2 tiếp tuyến cắt nhau)

$\Rightarrow OM$ là trung trực của $AB$

$\Rightarrow H$ là trung điểm của $AB$

$\Rightarrow AB=2AH=2.4,33=8,66$ (m)

$S_{MAB}=\frac{MH.AB}{2}=\frac{7,5.8,66}{2}=32,475$ (m²)

Answer 2

Hình vẽ: