H cách A cố định một khoảng bằng OA không đổi nên H di chuyển trên đường tròn (A; AO).

H cách A cố định một khoảng bằng OA không đổi nên H di chuyển trên đường tròn (A; AO).
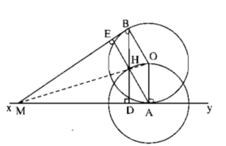
Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB. Tứ giác AOBH là hình gì?
Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB. Chứng minh rằng ba điểm M, H, O thẳng hàng.
Cho đường tròn (O) và tiếp tuyến tại A của đường tròn đó. từ một điểm M bất kì trên tiếp tuyến này ta kẻ tiếp tuyến MB với (O).
a. c/m OAMB nội tiếp.
b. Gọi H là trực tâm của tam giác MAB. C/m OAHB là hình thoi.
c. Khi M di động trên tiếp tuyến A thì tâm đường tròn ngoại tiếp tam giác MAB chạy trên đường nào?
Cho đường tròn tâm O, đường lính AB. Gọi M là điểm tuyd ý trên đường tròn, xy là tiếp tuyến của đường tròn tại A. Qua M kẻ MP vuông góc với AB, MQ vuồn góc với xy
a, tứ giác APMQ là hình gì? vì sao?
b, gọi I là trung điểm của PQ. chứng minh OQ vuông góc với AM
c, khi điểm M di chuyển trên đường tròn tâm O thì I chuyển động trên đường nào? vì sao?
Cho đường tròn ( O; R ) , điểm A cố định nằm trên đường tròn , kẻ tiếp tuyến d qua A với ( O ) . Trên d lấy điểm M ( M khác A ) , từ M kẻ tiếp tuyến thứ 2 là MB với ( O ) ( B là tiếp điểm )
a, CM 4 điểm A , O , B , M cùng nằm trên 1 đt
b , Đoạn OM cắt đtròn ( O ) tại I . Chứng minh BI là phân giác của góc MAB . Từ đó suy ra I là tâm của đtròn nội tiếp tam giác MAB
c, gọi H là trực tâm của tam giác MAB . Điểm H chạy trên đường nào khi M chạy trên d
Bài 1: Cho dường tròn tâm O đường kính AB; M là một điểm di động trên đường tròn( m khác A và B). Dựng đường tròn tâm M tiếp xúc với Ab tại H. Từ A và B kể tiếp tuyến BD và AC đến đường tròn tâm M.
a)Xác định vị trí tương đối của đường thẳng CD và đường tròn tâm O.
b) Tìm vị trí của M trên (O) để AC.BD đạt ghía trị lớn nhất.
c).lấy N là điểm cố định trên đường tròn (O); Gọi I là trung điểm của MN; P là hình chiếp của I trên MB; Khi M di chuyển trên (O) thì P chạy trên đường nào
Bài 1: Cho dường tròn tâm O đường kính AB; M là một điểm di động trên đường tròn( m khác A và B). Dựng đường tròn tâm M tiếp xúc với Ab tại H. Từ A và B kể tiếp tuyến BD và AC đến đường tròn tâm M.
a)Xác định vị trí tương đối của đường thẳng CD và đường tròn tâm O.
b) Tìm vị trí của M trên (O) để AC.BD đạt ghía trị lớn nhất.
c).lấy N là điểm cố định trên đường tròn (O); Gọi I là trung điểm của MN; P là hình chiếp của I trên MB; Khi M di chuyển trên (O) thì P chạy trên đường nào
Cho đường tròn (O) và đường thẳng xy không có điểm chung với đường tron f(O). Gọi A là hình chiếu của O trên đường thẳng xy. Qua A vẽ cát tuyến không đi qua O cắt đường tròn tại hai điểm B và C (AB < AC). Tiếp tuyến của đường tròn tại hai điểm B và C cắt đường thẳng xy lần lượt taiij M và N.
a) Chứng minh tứ giác ABOM nội tiếp.
b) Chứng minh góc BCO bằng góc ANO và tam giác OMN cân.
c) Giả sử đường tròn (O) và đường thẳng xy cố định. Từ M vẽ tiếp tuyến thứ hai ME với đường tròn (O), E là tiếp điểm khác B. Chứng minh khi cát tuyến ABC di chuyển quanh A thì BE luôn đi qua một điểm cố định.
GIÚP MÌNH CÂU C VỚI!!!
Cho đường tròn tâm O có đường kính AB R2 . Gọi M là điểm di động trên đường tròn O . Điểm M khác AB, ; dựng đường tròn tâm M tiếp xúc với AB tại H . Từ A và B kẻ hai tiếp tuyến AC và BD với đường tròn tâm M vừa dựng.
a) Chứng minh BM AM , lần lượt là các tia phân giác của các góc ABD và BAC .
b) Chứng minh ba điểm C M D , , nằm trên tiếp tuyến của đường tròn tâm O tại điểm M .
c) Chứng minh AC BD không đổi, từ đó tính tích AC BD. theo CD .
d) Giả sử ngoài AB, trên nửa đường tròn đường kính AB không chứa M có một điểm N cố định. gọi I là trung điểm của MN , kẻ IP vuông góc với MB . Khi M chuyển động thì P chuyển động trên đường cố định nào.
Cần giải câu d