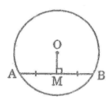
Áp dụng định lí Pitago vào tam giác vuông OMB ta có:
O B 2 = O M 2 + M B 2
Suy ra: M B 2 = O B 2 - O M 2 = 5 2 - 1 , 4 2 = 25 - 1,96 = 23,04
MB = 4,8 (cm)
Vậy AB = 2.MB = 2.4,8 = 9,6 (cm)

Áp dụng định lí Pitago vào tam giác vuông OMB ta có:
O B 2 = O M 2 + M B 2
Suy ra: M B 2 = O B 2 - O M 2 = 5 2 - 1 , 4 2 = 25 - 1,96 = 23,04
MB = 4,8 (cm)
Vậy AB = 2.MB = 2.4,8 = 9,6 (cm)
Cho đường tròn tâm O, bán kính R và M là một điểm nằm bên ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm). Gọi E là giao điểm của AB và OM.
a) Chứng minh tứ giác MAOB nội tiếp được trong một đường tròn.
b) Tính độ dài đoạn thẳng AB và ME biết OM = 5cm và R = 3cm.
c) Kẻ tia Mx nằm trong góc AMO cắt đường tròn tại 2 điểm phân biệt C và D (C nằm giữa M và D). Chứng minh rằng góc MEC = góc OED
Cho đường tròn (O; R) và điểm M bất kì, biết rằng OM = R . Chọn khẳng định đúng?
A. Điểm M nằm ngoài đường tròn (O; R)
B. Điểm M nằm trên đường tròn (O; R)
C.Điểm M nằm trong đường tròn (O; R)
D. Điểm M không thuộc đường tròn (O; R)
Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn . Từ A kẻ tiếp tuyến AE đến đường tròn (O) (với E là tiếp điểm) . Vẽ dây EH vuông góc với AO tại M.
a) Cho biết bán kính R`=5cm`; OM`=3cm`. Tính độ dài dây EH
b) Chứng minh AH là tiếp tuyến của đường tròn (O)
c) Đường thẳng qua O vuông góc với OA cắt AH tại B . Vẽ tiếp tuyến BF với đường tròn (O) (F là tiếp điểm) . Chứng minh 3 điểm E,O,F thẳng hàng và BF.AE`=R^2`
* vẽ hình và làm bài trên
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là các tiếp điểm). Tính độ dài các cạnh của tam giác AMN biết OM = 3cm, OA = 5cm
Câu 4:( 4 điểm ) Từ điểm M nằm ngoài đường tròn ( O,R ) sao cho OM = 3R, vẽ các tiếp tuyến MA, MB với đường tròn ( O,R ) (A, B là các tiếp điểm). a ) Chứng minh: Tứ giác MAOB nội tiếp và OM là đường trung trực của đoạn AB. b ) Tính độ dài đoạn thẳng MA, AB theo R. c) Vẽ dây AC song song MB, đường thẳng MC cắt đường tròn (O,R) tại điểm thứ hai là D, tia AD cắt MB tại E. Chứng minh: E là trung điểm của đoạn MB
Từ 1 điểm M nằm ở bên ngoài đường tròn O bán kính R, vẽ các tiếp tuyến MA. MB với đường tròn( A, B là các tiếp điểm). vẽ cát tuyến MCD không đi qua tâm O của đường tròn( C nằm giữa M và D)Gọi E là trung điểm CD
a) Chứng minh 5 điểm M,A,B,E,O cùng thuộc 1 đường tròn
b)Trong trường hợp OM = 2R và C là trung điểm của MD>hãy tính độ dài MD theo R
c)Chứng minh hệ thức CD^2 = 4AE.BE
Từ 1 điểm M nằm ở bên ngoài đường tròn O bán kính R, vẽ các tiếp tuyến MA. MB với đường tròn( A, B là các tiếp điểm). vẽ cát tuyến MCD không đi qua tâm O của đường tròn( C nằm giữa M và D)Gọi E là trung điểm CD
a) Chứng minh 5 điểm M,A,B,E,O cùng thuộc 1 đường tròn
b)Trong trường hợp OM = 2R và C là trung điểm của MD>hãy tính độ dài MD theo R
c)Chứng minh hệ thức CD^2 = 4AE.BE
Bài 1:
Cho (O;R), và một điểm M nằm ngoài đường tròn (O) sao cho OM = 2R. Từ M vẽ tiếp
tuyến MA của đường tròn (O) (A là tiếp điểm)
a) Tính độ dài AM theo R
b) Từ A kẻ dây cung AB vuông góc với OM tại H. Chứng minh MB là tiếp tuyến của
đường tròn (O)
(vẽ hình)
Cho đường tròn (O; R) và hai tiếp tuyến MA, MB cắt nhau tại M (A, B là các tiếp tuyến điểm). a) Chứng minh rằng OM vuông góc AB. b) Gọi H là giao điểm của OM và AB. Cho bán kính dường tròn bằng 13cm, OH = 5cm Tính độ dàiAB.