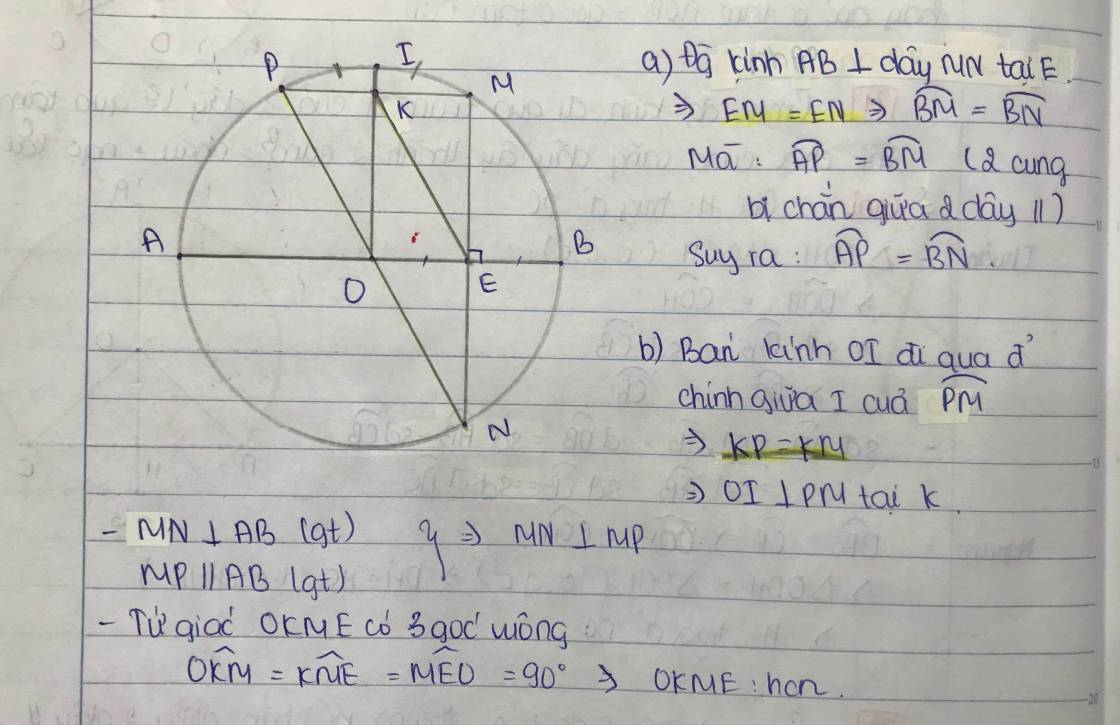
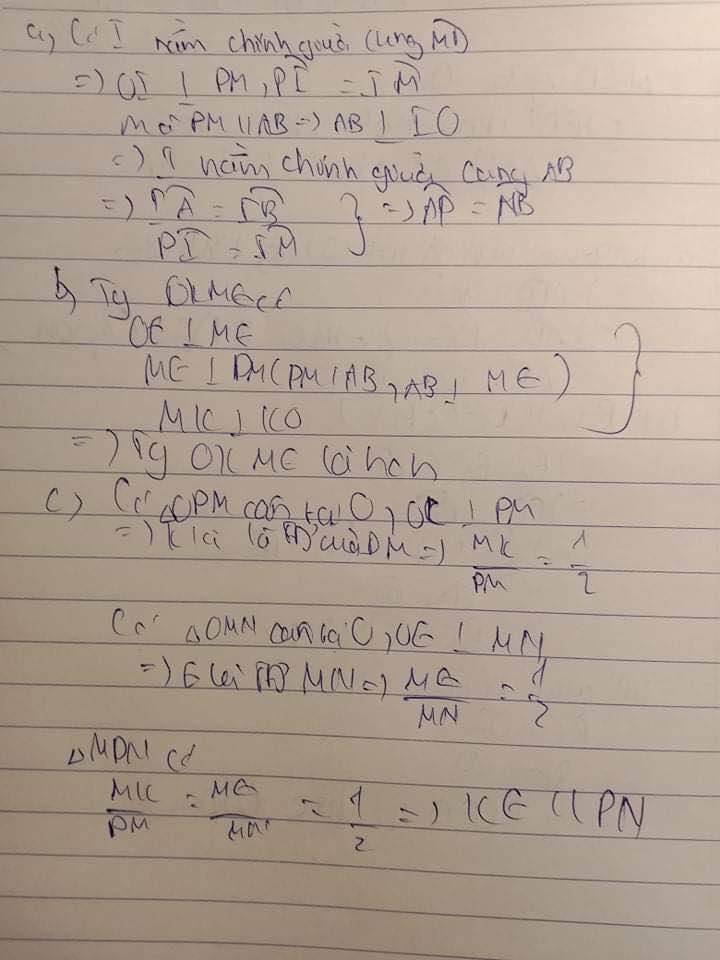Cho đường tròn (O) đường kính AB. Qua trung điểm E của OB kẻ một đường thẳng vuông góc với OB, cắt đường tròn (O) ở M và N. Kẻ dây MP song song với AB. Gọi I là điểm chính giữa của cung nhỏ PM. Gọi K là giao điểm của OI và PM. Chứng minh rằng:
a) \(\stackrel\frown{AP}=\stackrel\frown{BN}\).
b) Tứ giác $OKME$ là hình chữ nhật.
c) Ba điểm $P,$ $O,$ $N$ thẳng hàng và $KE // PN$.
Thọ tested! h heeeee
\(\sqrt{2222}\)
\(\dfrac{1}{22}\)
Giải :
a) Xét (O) có PM // AB
⇒ 2 cung AP và BM bị chắn bởi 2 dây trên sẽ bằng nhau.
mà BM = BN ( △ BMN cân tại B vì có BE vừa là đ/c, đường trung tuyến △)
⇒ cung BM = cung BN
⇒ cung AP = cung BN
b) Xét (O) có OI đi qua điểm chính giữa của PM (gt)
⇒ OI vuông góc với dây PM tại K
⇒góc OKM = 90 độ.
Xét tứ giác OKME có 3 góc vuông : góc OKM = 90 độ (cmt),
góc MEO = 90 độ ( MN vuông góc với OB tại E
góc EMK = 90 độ ( vì PM//AB, AB vuông góc với MN ⇒ PM vuông góc với MN tại M )
⇒ OKME là hcn
c) Ta có : góc OPI = góc NOE ( vì 2 góc đông vị, MP//AB)
mà góc OPI + góc POI = 90 độ ( △POK vuông tại K )
⇒góc NOE + góc POI = 90 độ
⇒ góc NOE + góc POI + góc IOE = 90 + 90 = 180 độ
⇒ P,O,N thẳng hàng
- Xét △ PMN có KE đường TB ( K trđ PM, E trđ MN )
⇒ KE//PN
a) CÓ PM //AB
=> CUNG AP= CUNG MB ( TÍNH CHẤT) (1)
MÀ CM ĐƯỢC B LÀ ĐIỂM CHÍNH GIỮA CUNG MN => CUNG MB=CUNG NB (2)
TỪ (1) (2) => CUNG AP= CUNG NB
b) CM ĐƯỢC KME=90 ĐỘ ( VÌ PM //AB MÀ AB VUÔNG GÓC MN )
VÌ I LÀ ĐIỂM CHÍNH GIỮA CUNG PM => OI VUÔNG GÓC PM TẠI K => OKM = 90 ĐỘ
TỨ GIÁC OKME CÓ OKM=KME=MEO=90 ĐỘ => TỨ GIÁC OKME LÀ HÌNH CHỮ NHẬT
c) CHỨNG MINH ĐƯỢC KE LÀ ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC PMN => KE // PN
MẶT KHÁC CÓ OK=ME=NE MÀ NE//OK (CÙNG VUÔNG GÓC AB )
=> TỨ GIÁC OKNE LÀ HÌNH BÌNH HÀNH => KE//ON
CÓ KE//ON MÀ KE//PN NÊN PN TRÙNG ON => O, P, N THẲNG HÀNG
a) Xét đường tròn (O) có: \(AB\perp MN\) tại E(GT)
=> EM = EN; cung BM= cung BN
Lại có: cung AP = cung BM ( 2 cung nằm giữa 1 dây song song thì bằng nhau )
=> cung AP = cung BN (đpcm)
b) Xét đường tròn (O) có OI đi qua điểm chính giữa I của cung OM
=> KP = KM và \(OI\perp PM\) tại K=> OKM = 90°
mà \(MN\perp AB\) (GT)
MP // AB (GT)
=> \(MN\perp MP\) => NMP = 90° hay EMK = 90°
Ta có: \(MN\perp AB\) (GT) =>MEA= 90° hay MEO = 90°
Xét tứ giác OKME có: OKM = 90° (cmt)
EMK = 90°(cmt)
MEO = 90°(cmt)
=> tứ giác OKME là hình chữ nhật (dhnb) (đpcm)
c) * Vì cung AP = cung BN ( câu a)
=> AOP = BON
mà 3 điểm A,O,B thẳng hàng nên 3 điểm P,O,N cũng thẳng hàng ( đpcm )
* Xét \(\Delta MNP\) có: EM = EN ( câu a )
KP = KM ( câu b)
=> KE là đường trung bình của \(\Delta MNP\)
=> KE // PN ( đpcm )
a, có I nằm chính giữa cung MD
=> OI vuông góc với PM, cung PI=cung IM
mà PM song song với AB =>AB vuông góc với IO
=> I nằm chính giữa cung AB
=> cung IA = cung IB
mà cung PI =cung IM
=>cung AP = cung MB
b,xét tứ giác OKME có
OE vuông góc với ME
ME vuông góc với PM
MK vuông góc ới KO
=> tứ giác OKME là hình chữ nhật
c,có tam giác OMN cân tại ,OK vuông góc với PM
ð K là trung điểm MN =>ME/MN=1/2
ð Xét tam giác MPN có
ð MK/PM = ME/MN=1/2
ð KE//PN
a) Xét (O) có PM // AB
⇒ 2 cung AP và BM bị chắn bởi 2 dây trên sẽ bằng nhau.
mà BM = BN ( △ BMN cân tại B vì có BE vừa là đ/c, đường trung tuyến △)
⇒ cung BM = cung BN
⇒ cung AP = cung BN
b) Xét (O) có OI đi qua điểm chính giữa của PM (gt)
⇒ OI vuông góc với dây PM tại K
⇒góc OKM = 90 độ.
Xét tứ giác OKME có 3 góc vuông : góc OKM = 90 độ (cmt),
góc MEO = 90 độ ( MN vuông góc với OB tại E
góc EMK = 90 độ ( vì PM//AB, AB vuông góc với MN ⇒ PM vuông góc với MN tại M )
⇒ OKME là hcn
c) Ta có : góc OPI = góc NOE ( vì 2 góc đông vị, MP//AB)
mà góc OPI + góc POI = 90 độ ( △POK vuông tại K )
⇒góc NOE + góc POI = 90 độ
⇒ góc NOE + góc POI + góc IOE = 90 + 90 = 180 độ
⇒ P,O,N thẳng hàng
- Xét △ PMN có KE đường TB ( K trung điểm PM, E trung điểm MN )
⇒ KE//PN
a.Xét tam giác POM có:cung PI=cung PM
=>OI là phân giác góc POM
Ta có:góc POA+góc POM+góc MOB=180 độ
Mà góc POA+góc PIO=góc IOM+góc MOB
mà góc PIO=góc IOM
=>góc POA=góc MOB (1)
vì OB là đường kính đi qua trung điểm E của MN
=>OB là phân giác góc MON
=>góc MOB=BON (2)
Từ (1),(2) ta suy ra:góc POA=góc NOB
Mà 2 góc đều xuất phát từ tâm (O) của đường tròn
=>AP=BN
b.Vì góc POA=góc NOB
Mà A,O,B thẳng hàng => P,O,N thẳng hàng
=>PN là đường kính đường tròn (O)
xét tam giác PMN có PN là đường kính
=>tam giác PMN vuông tại M=>IME=90 độ
xét tứ giác IMEO có:góc IOE=góc OEM=góc IME=90 độ
=>IMEO là hình chữ nhật
c.Đã chứng minh ở câu b P,O,N thẳng hàng
Vì KMEO là hcn=>góc IOM=góc KEM
Ta có:góc IOM=cung IM=1/2 cung PM(vì I là điểm chính giữa cung PM) (3)
góc POM=1/2 cung PM (4)
Từ (3),(4) ta suy ra:góc IOM=POM
Mà góc KOM=góc KEM
=>góc KEM=góc PNM
=>KE//PN
a) Xét (O) có PM // AB
⇒ 2 cung AP và BM bị chắn bởi 2 dây trên sẽ bằng nhau.
mà BM = BN ( △ BMN cân tại B vì có BE vừa là đ/c, đường trung tuyến △)
⇒ cung BM = cung BN
⇒ cung AP = cung BN
b) Xét (O) có OI đi qua điểm chính giữa của PM (gt)
⇒ OI vuông góc với dây PM tại K
⇒góc OKM = 90 độ.
Xét tứ giác OKME có 3 góc vuông : góc OKM = 90 độ (cmt),
góc MEO = 90 độ ( MN vuông góc với OB tại E
góc EMK = 90 độ ( vì PM//AB, AB vuông góc với MN ⇒ PM vuông góc với MN tại M )
⇒ OKME là hcn
c) Ta có : góc OPI = góc NOE ( vì 2 góc đông vị, MP//AB)
mà góc OPI + góc POI = 90 độ ( △POK vuông tại K )
⇒góc NOE + góc POI = 90 độ
⇒ góc NOE + góc POI + góc IOE = 90 + 90 = 180 độ
⇒ P,O,N thẳng hàng
- Xét △ PMN có KE đường TB ( K trđ PM, E trđ MN )
⇒ KE//PN
a) Xét (O) có PM // AB
⇒ 2 cung AP và BM bị chắn bởi 2 dây trên sẽ bằng nhau.
mà BM = BN ( △ BMN cân tại B vì có BE vừa là đ/c, đường trung tuyến △)
⇒ cung BM = cung BN
⇒ cung AP = cung BN
b) Xét (O) có OI đi qua điểm chính giữa của PM (gt)
⇒ OI vuông góc với dây PM tại K
⇒góc OKM = 90 độ.
Xét tứ giác OKME có 3 góc vuông : góc OKM = 90 độ (cmt),
góc MEO = 90 độ ( MN vuông góc với OB tại E
góc EMK = 90 độ ( vì PM//AB, AB vuông góc với MN ⇒ PM vuông góc với MN tại M )
⇒ OKME là hcn
c) Ta có : góc OPI = góc NOE ( vì 2 góc đông vị, MP//AB)
mà góc OPI + góc POI = 90 độ ( △POK vuông tại K )
⇒góc NOE + góc POI = 90 độ
⇒ góc NOE + góc POI + góc IOE = 90 + 90 = 180 độ
⇒ P,O,N thẳng hàng
- Xét △ PMN có KE đường TB ( K trđ PM, E trđ MN )
⇒ KE//PN
a)Có I nằm chính giữa cung MP
⇒ OI⊥PM , cung PI= cung IM
mà PM//AB ⇒AB⊥IO
⇒ I nằm chính giữa cung AB
⇒IA=IB, mà cung PI= cung IM
⇒AP=MB
b) Xét tứ giác OKME có:
OE ⊥ ME
ME⊥PM
MK⊥KO
⇒ Tứ hiacs OKME à hcn
a) Xét (O) có PM // AB
⇒ 2 cung AP và BM bị chắn bởi 2 dây trên sẽ bằng nhau.
mà BM = BN ( △ BMN cân tại B vì có BE vừa là đ/c, đường trung tuyến △)
⇒ cung BM = cung BN
⇒ cung AP = cung BN
b) Xét (O) có OI đi qua điểm chính giữa của PM (gt)
⇒ OI vuông góc với dây PM tại K
⇒góc OKM = 90 độ.
Xét tứ giác OKME có 3 góc vuông : góc OKM = 90 độ (cmt),
góc MEO = 90 độ ( MN vuông góc với OB tại E
góc EMK = 90 độ ( vì PM//AB, AB vuông góc với MN ⇒ PM vuông góc với MN tại M )
⇒ OKME là hcn
c) Ta có : góc OPI = góc NOE ( vì 2 góc đông vị, MP//AB)
mà góc OPI + góc POI = 90 độ ( △POK vuông tại K )
⇒góc NOE + góc POI = 90 độ
⇒ góc NOE + góc POI + góc IOE = 90 + 90 = 180 độ
⇒ P,O,N thẳng hàng
- Xét △ PMN có KE đường TB ( K trđ PM, E trđ MN )
⇒ KE//PN
a) Xét (O) có PM // AB
⇒ 2 cung AP và BM bị chắn bởi 2 dây trên sẽ bằng nhau.
mà BM = BN ( △ BMN cân tại B vì có BE vừa là đ/c, đường trung tuyến △)
⇒ cung BM = cung BN
⇒ cung AP = cung BN
b) Xét (O) có OI đi qua điểm chính giữa của PM (gt)
⇒ OI vuông góc với dây PM tại K
⇒góc OKM = 90 độ.
Xét tứ giác OKME có 3 góc vuông : góc OKM = 90 độ (cmt),
góc MEO = 90 độ ( MN vuông góc với OB tại E
góc EMK = 90 độ ( vì PM//AB, AB vuông góc với MN ⇒ PM vuông góc với MN tại M )
⇒ OKME là hcn
c) Ta có : góc OPI = góc NOE ( vì 2 góc đông vị, MP//AB)
mà góc OPI + góc POI = 90 độ ( △POK vuông tại K )
⇒góc NOE + góc POI = 90 độ
⇒ góc NOE + góc POI + góc IOE = 90 + 90 = 180 độ
⇒ P,O,N thẳng hàng
- Xét △ PMN có KE đường TB ( K trđ PM, E trđ MN )
⇒ KE//PN
a) Xét (O) có PM // AB
⇒ 2 cung AP và BM bị chắn bởi 2 dây trên sẽ bằng nhau.
mà BM = BN ( △ BMN cân tại B vì có BE vừa là đ/c, đường trung tuyến △)
⇒ cung BM = cung BN
⇒ cung AP = cung BN
b) Xét (O) có OI đi qua điểm chính giữa của PM (gt)
⇒ OI vuông góc với dây PM tại K
⇒góc OKM = 90 độ.
Xét tứ giác OKME có 3 góc vuông : góc OKM = 90 độ (cmt),
góc MEO = 90 độ ( MN vuông góc với OB tại E
góc EMK = 90 độ ( vì PM//AB, AB vuông góc với MN ⇒ PM vuông góc với MN tại M )
⇒ OKME là hcn
c) Ta có : góc OPI = góc NOE ( vì 2 góc đông vị, MP//AB)
mà góc OPI + góc POI = 90 độ ( △POK vuông tại K )
⇒góc NOE + góc POI = 90 độ
⇒ góc NOE + góc POI + góc IOE = 90 + 90 = 180 độ
⇒ P,O,N thẳng hàng
- Xét △ PMN có KE đường TB ( K trđ PM, E trđ MN )
⇒ KE//PN
a) Xét (O) có PM // AB
⇒ 2 cung AP và BM bị chắn bởi 2 dây trên sẽ bằng nhau.
mà BM = BN ( △ BMN cân tại B vì có BE vừa là đường cao, đường trung tuyến △)
⇒ cung BM = cung BN
⇒ cung AP = cung BN
b) Xét (O) có OI đi qua điểm chính giữa của PM (gt)
⇒ OI vuông góc với dây PM tại K
⇒góc OKM = 90 độ.
Xét tứ giác OKME có 3 góc vuông : góc OKM = 90 độ (cmt),
góc MEO = 90 độ ( MN vuông góc với OB tại E
góc EMK = 90 độ ( vì PM//AB, AB vuông góc với MN ⇒ PM vuông góc với MN tại M )
⇒ OKME là hcn
c) Ta có : góc OPI = góc NOE ( vì 2 góc đông vị, MP//AB)
mà góc OPI + góc POI = 90 độ ( △POK vuông tại K )
⇒góc NOE + góc POI = 90 độ
⇒ góc NOE + góc POI + góc IOE = 90 + 90 = 180 độ
⇒ P,O,N thẳng hàng
- Xét △ PMN có KE là đường TB ( K trung điểm PM, E trung điểm MN )
⇒ KE//PN
a) Xét (O) có PM // AB
⇒ 2 cung AP và BM bị chăn bởi 2 dây trên sẽ băng nhau.
mà BM = BN (△BMN cân tại B vì có BE vừa là đ/c, đường trung tuyên △)
⇒ cung BM = cung BN
⇒ cung AP = cung BN
b) Xét (O) có OI đi qua điểm chính giữa của PM (gt)
⇒ OI vuông góc với dây PM tại K
⇒góc OKM = 90o
Xét tứ giác OKME có 3 góc vuông : góc OKM = 90 độ (cmt),
góc MEO = 90o ( MN vuông góc với OB tại E
góc EMK = 900 ( vì PM//AB, AB vuông góc với MN ⇒ PM vuông góc với MN tại M )
⇒ OKME là hcn
c) Ta có : góc OPI = góc NOE ( vì 2 góc đông vị, MP//AB)
mà góc OPI + góc POI = 90 độ ( △POK vuông tại K )
⇒góc NOE + góc POI = 900
⇒ góc NOE + góc POI + góc IOE = 900 + 900 = 1800
⇒ P,O,N thẳng hàng
- Xét △ PMN có KE đường TB (K trung điểm PM, E trung điểm MN )
⇒ KE//PN
a) Xét (O) có PM // AB
⇒ 2 cung AP và BM bị chắn bởi 2 dây trên sẽ bằng nhau.
mà BM = BN ( △ BMN cân tại B vì có BE vừa là đ/c, đường trung tuyến △)
⇒ cung BM = cung BN
⇒ cung AP = cung BN
b) Xét (O) có OI đi qua điểm chính giữa của PM (gt)
⇒ OI vuông góc với dây PM tại K
⇒góc OKM = 90 độ.
Xét tứ giác OKME có 3 góc vuông : góc OKM = 90 độ (cmt),
góc MEO = 90 độ ( MN vuông góc với OB tại E
góc EMK = 90 độ ( vì PM//AB, AB vuông góc với MN ⇒ PM vuông góc với MN tại M )
⇒ OKME là hcn
c) Ta có : góc OPI = góc NOE ( vì 2 góc đông vị, MP//AB)
mà góc OPI + góc POI = 90 độ ( △POK vuông tại K )
⇒góc NOE + góc POI = 90 độ
⇒ góc NOE + góc POI + góc IOE = 90 + 90 = 180 độ
⇒ P,O,N thẳng hàng
- Xét △ PMN có KE đường TB ( K trđ PM, E trđ MN )
⇒ KE//PN