Cho đường tròn \(\left(O;R\right)\) và 2 đường kính \(AB\) và \(CD\) sao cho tiếp tuyến tại \(A\) của đường tròn \(\left(O;R\right)\) cắt các đường thẳng \(BC\) và \(BD\) tại hai điểm tương ứng là \(E\) và \(F\). Gọi \(P\) và \(Q\) lần lượt là trung điểm của các đoạn thẳng \(AE\) và \(AF\).
\(a\)) Chứng minh rằng trực tâm \(H\) của tam giác \(BPQ\) là trung điểm của đoạn thẳng \(OA\).
\(b\)) Gọi \(\alpha\) là số đo góc \(BFE\). Hai đường kính \(AB\) và \(CD\) thỏa mãn điều kiện gì thì biểu thức: \(P=\sin^6\alpha+\cos^6\alpha\) đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
\(c\)) Chứng minh các hệ thức sau: \(CE\cdot DF\cdot EF=CD^3\) và \(\dfrac{BE^3}{BF^3}=\dfrac{CE}{DF}\)
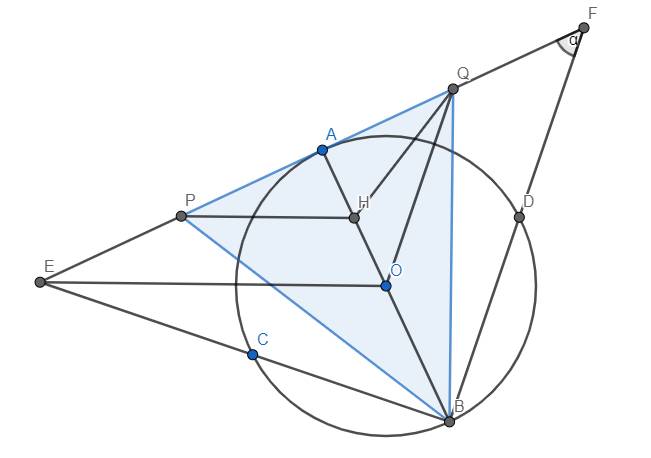
a) Định nghĩa lại H là trung điểm OA. Ta thấy OQ là đường trung bình của tam giác ABF nên OQ//BF. Hơn nữa \(BF\perp BE\) nên \(OQ\perp BE\). Lại có \(BA\perp QE\) nên O là trực tâm của tam giác BEQ \(\Rightarrow OE\perp BQ\)
Mặt khác, PH là đường trung bình của tam giác AOE nên PH//OA. Do đó, \(PH\perp BQ\). Lại thấy rằng \(BH\perp PQ\) nên H là trực tâm tam giác BPQ (đpcm)
b) Ta có \(P=\sin^6\alpha+\cos^6\alpha\)
\(=\left(\sin^2\alpha\right)^3+\left(\cos^2\alpha\right)^3\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)\left(\sin^4\alpha+\cos^4\alpha-\sin^2\alpha\cos^2\alpha\right)\)
\(=1.\left[\left(\sin^2\alpha+\cos^2\alpha\right)^2-3\sin^2\alpha\cos^2\alpha\right]\)
\(=1-3\sin^2\alpha\cos^2\alpha\)
\(\le1-3.\dfrac{\left(\sin^2\alpha+\cos^2\alpha\right)^2}{4}\)
\(=\dfrac{1}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow\sin\alpha=\cos\alpha\) \(\Leftrightarrow\alpha=45^o\) hay 2 dây AB, CD vuông góc với nhau.
Vậy \(min_P=\dfrac{1}{4}\)
c) Ta có \(\left\{{}\begin{matrix}EC.EB=EA^2\\FD.FB=FA^2\end{matrix}\right.\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow EC.EB.FD.FB=\left(EA.FA\right)^2\)
\(\Rightarrow EC.FD.\left(EB.DB\right)=AB^4\)
\(\Rightarrow EC.FD.\left(EF.AB\right)=AB^4\)
\(\Rightarrow EC.FD.EF=AB^3=CD^3\) (đpcm)
Ta có \(EC.DF=AC.AD=BC.BD\)
\(\Rightarrow\dfrac{EC}{DF}=\dfrac{BC.BD}{DF^2}\)
\(=\dfrac{BC}{DF}.\dfrac{BD}{DF}\)
\(=\dfrac{BE}{BF}.\dfrac{AC}{DF}\)
\(=\dfrac{BE}{BF}.\dfrac{AE}{AF}\)
\(=\left(\dfrac{BE}{BF}\right)^3\)
Ta có đpcm.
Bài khá căng đấy













