Các câu hỏi tương tự
Cho tam giác SAB vuông tại A, ABS 60
°
đường phân giác trong của ABS cắt SA tại điểm I. Vẽ nửa đường tròn tâm I bán kính IA (như hình vẽ). Cho
∆
S
A
B
và nửa đường tròn trên quay quanh cạnh SA tạo nên các khối tròn xoay tương ứng có thể tích
V
1
,
V
2
. Khẳng định nào dưới đây đúng? A.
4
V
1...
Đọc tiếp
Cho tam giác SAB vuông tại A, ABS = 60 ° đường phân giác trong của ABS cắt SA tại điểm I. Vẽ nửa đường tròn tâm I bán kính IA (như hình vẽ). Cho ∆ S A B và nửa đường tròn trên quay quanh cạnh SA tạo nên các khối tròn xoay tương ứng có thể tích V 1 , V 2 . Khẳng định nào dưới đây đúng?
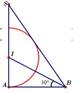
A. 4 V 1 = 9 V 2
B. 9 V 1 = 4 V 2
C. V 1 = 3 V 2
D. 2 V 1 = 3 V 2
Cho nửa đường tròn đường kính AB, điểm C nằm trên nửa đường tròn này sao cho góc BAC bằng
30
°
, đồng thời cho nửa đường tròn đường kính AD (xem hình vẽ). Tính thểt ích V của khối tròn xoay được tạo thành khi quay hình phẳng (H) (phần tô đậm) xung quanh đường thẳng AB, biết rằng
A
B
2
A
D
và nửa hình tròn đường kính AB có diện tích bằng
32
π
. A.
V
87...
Đọc tiếp
Cho nửa đường tròn đường kính AB, điểm C nằm trên nửa đường tròn này sao cho góc BAC bằng 30 ° , đồng thời cho nửa đường tròn đường kính AD (xem hình vẽ). Tính thểt ích V của khối tròn xoay được tạo thành khi quay hình phẳng (H) (phần tô đậm) xung quanh đường thẳng AB, biết rằng A B = 2 A D và nửa hình tròn đường kính AB có diện tích bằng 32 π .
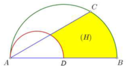
A. V = 874 3 π
B. V = 847 3 π
C. V = 784 3 π
D. V = 438 π
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần màu vàng nhạt (hình vẽ bên dưới) quay quanh đường thẳng AD bằng A.
23
π
a
3
3
216
B.
π
a
3...
Đọc tiếp
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần màu vàng nhạt (hình vẽ bên dưới) quay quanh đường thẳng AD bằng
A. 23 π a 3 3 216
B. π a 3 3 24
C. 20 π a 3 3 217
D. 4 π a 3 3 27
Cho tam giác ABC đều cạnh 3 và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần tô đậm (hình vẽ bên) quay quanh đường thẳng AD bằng A.
V
9
3
8
π
B.
V
23
3
8
π
C.
V...
Đọc tiếp
Cho tam giác ABC đều cạnh 3 và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần tô đậm (hình vẽ bên) quay quanh đường thẳng AD bằng
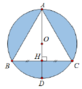
A. V = 9 3 8 π
B. V = 23 3 8 π
C. V = 23 3 24 π
D. V = 5 3 8 π
Cho tam giác ABC đều cạnh 3 và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần tô đậm (hình vẽ bên) quay quanh đường thẳng AD bằng A.
V
9
3
8
π
B.
V
23
3
8...
Đọc tiếp
Cho tam giác ABC đều cạnh 3 và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần tô đậm (hình vẽ bên) quay quanh đường thẳng AD bằng
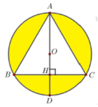
A. V = 9 3 8 π
B. V = 23 3 8 π
C. V = 23 3 24 π
D. V = 5 3 8 π
Trong không gian cho hình tròn đường kính 4a quay quanh đường kính của nó. Khi đó thể tích khối tròn xoay sinh ra bằng
Đọc tiếp
Trong không gian cho hình tròn đường kính 4a quay quanh đường kính của nó. Khi đó thể tích khối tròn xoay sinh ra bằng
![]()
![]()
![]()
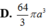
Cho nửa đường tròn đường kính
A
B
4
5
. Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hai điểm cách nhau 4 cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4 cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần tô màu trong hình vẽ). Đem phần còn lại quay quanh trục AB. Thể tích của khối tròn...
Đọc tiếp
Cho nửa đường tròn đường kính A B = 4 5 . Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hai điểm cách nhau 4 cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4 cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần tô màu trong hình vẽ). Đem phần còn lại quay quanh trục AB. Thể tích của khối tròn xoay thu được bằng:
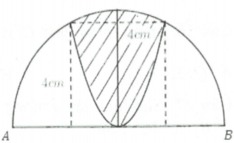
A. V = π 15 800 5 - 464 c m 3
B. V = π 3 800 5 - 928 c m 3
C. V = π 5 800 5 - 928 c m 3
D. V = π 15 800 5 - 928 c m 3
Cho tam giác SAB vuông tại A,
∠
A
B
S
60
°
. Phân giác của góc
∠
A
B
S
cắt SA tại I. Vẽ nửa đường tròn tâm I, bán kính IA (như hình vẽ). Cho miền tam giác SAB và nửa hình tròn quay xung quanh trục SA tạo nên các khối tròn xoay có thể tích tương ứng là V1, V2. Khẳng định nào sau đây là đúng? A.
V
1...
Đọc tiếp
Cho tam giác SAB vuông tại A, ∠ A B S = 60 ° . Phân giác của góc ∠ A B S cắt SA tại I. Vẽ nửa đường tròn tâm I, bán kính IA (như hình vẽ). Cho miền tam giác SAB và nửa hình tròn quay xung quanh trục SA tạo nên các khối tròn xoay có thể tích tương ứng là V1, V2. Khẳng định nào sau đây là đúng?
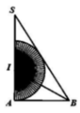
A. V 1 = 4 9 V 2
B. V 1 = 3 2 V 2
C. V 1 = 3 V 2
D. V 1 = 9 4 V 2
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng A.
4
π
a
3
3
27
B.
20
π...
Đọc tiếp
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng
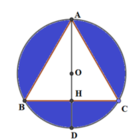
A. 4 π a 3 3 27
B. 20 π a 3 3 217
C. π a 3 3 24
D. 23 π a 3 3 216