Đáp án: C
(C): x 2 + y 2 = 9 có I(0;0), R = 3
Để Δ tiếp xúc với đường tròn (C) thì
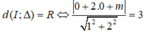
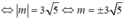
Đáp án: C
(C): x 2 + y 2 = 9 có I(0;0), R = 3
Để Δ tiếp xúc với đường tròn (C) thì
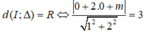
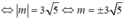
Cho hai đường thẳng d: 2x + y - 5 = 0; Δ: mx + (m - 2)y + 3 = 0. Giá trị của m để d và Δ vuông góc với nhau là:
A. m = 2 3
B. m = - 2 3
C. m = 2
D. m = - 2
Với giá trị nào của m thì đường thẳng Δ:3x– y+ 2m=0 tiếp xúc với đường tròn (C): x²+ y²+ 6x– 2y=0
a)Viết phương trình đường tròn đi qua 3 điểm A(-1;1);B(3;1);C(1;3)
b)Cho (C):x2+y2-4x+6y+3=0 và (Δ):3x-y+m=0.Tìm m để đường thẳng (Δ) tiếp xúc với đường tròn (C)
Trong mặt phẳng Oxy, cho điểm A(2;-4), đường thẳng Δ: x = -3 + 2t, y = 1 + t và đường tròn (C): x^2 + y^2 – 2x – 8y – 8 = 0.
a. Tìm một vectơ pháp tuyến n của đường thẳng Δ. Lập phương trình tổng quát của đường thẳng d, biết d đi qua điểm A và nhận n làm vectơ pháp tuyến.
b. Viết phương trình đường tròn (T), biết (T) có tâm A và tiếp xúc với Δ.
c. Gọi P, Q là các giao điểm của Δ và (C). Tìm toạ độ điểm M thuộc (C) sao cho tam giác MPQ cân tại M.
Với những giá trị nào của m thì đường thẳng ∆: 3x + 4y + 3= 0 tiếp xúc với đường tròn (C) : (x-m) 2+ y2 = 9
A. m= 0 và m= 1.
B. m= 4 và m= -6
C. m= 2
D. m= 6
Cho đường tròn (C): x 2 + y 2 + 4 x − 4 y − 10 = 0 và đường thẳng ∆: x + y + m = 0. Giá trị m để đường thẳng tiếp xúc với đường tròn là:
A. m = ± 6
B. m = ± 3
C. m = ± 8
D.Không tồn tại m
Cho M(5 ; 3) và ( Δ): 3x-4y+12=0. Lập phương trình đường tròn (C) bán kính R=5 đi qua M và (C) cắt ( Δ) tại A, B mà dt(MAB)max
Lập phương trình đường tròn (C) trong các trường hợp sau:
a, (C) có tâm I(-2; 3) và đi qua M(2; -3);
b, (C) có tâm I(-1; 2) và tiếp xúc với đường thẳng x – 2y +7 =0
c, (C) có đường kính AB với A = (1; 1) và B = (7; 5).