1 điểm M thuộc Δ là: M (-1; 3; 5) và 1 vecto chỉ phương của Δ là a → = (2;-3;4)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
viết phương trình tham số của dường thẳng Δ biết Δ vuông góc giá a→ và Δ vuông góc giá →b vecto a (0,1,2),vecto b(-1,3,2) và Δ đi qua gốc tọa độ
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
+
1
2
y
1
z
-
2
1
, mặt phẳng (P): x + y - 2z + 5 0 và A (1; -1; 2). Đường thẳng Δ cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn thẳng MN. Một vectơ chỉ phương của Δ là:...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x + 1 2 = y 1 = z - 2 1 , mặt phẳng (P): x + y - 2z + 5 = 0 và A (1; -1; 2). Đường thẳng Δ cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn thẳng MN. Một vectơ chỉ phương của Δ là:
A . u → = 2 ; 3 ; 2
B . u → = 1 ; - 1 ; 2
C . u → = - 3 ; 5 ; 1
D . u → = 4 ; 5 ; - 13
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2 ; 1 ; 0) và đường thẳng
∆
:
x
-
1
2
y
+
1
1
z
-
1
. Phương trình tham số của đường thẳng d đi qua M, cắt và vuông góc với Δ là:
A
.
d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2 ; 1 ; 0) và đường thẳng ∆ : x - 1 2 = y + 1 1 = z - 1 . Phương trình tham số của đường thẳng d đi qua M, cắt và vuông góc với Δ là:
A . d : x = 2 + t y = 1 - 4 t z = - 2 t
B . d : x = 2 - t y = 1 + t z = t
C . d : x = 1 + t y = - 1 - 4 t z = 2 t
D . d : x = 2 + 2 t y = 1 + t z = - t
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;1;0) và đường thẳng
∆
:
x
-
1
2
y
+
1
1
z
-
1
.Phương trình tham số của đường thẳng d đi qua M, cắt và vuông góc với Δ là:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;1;0) và đường thẳng ∆ : x - 1 2 = y + 1 1 = z - 1 .Phương trình tham số của đường thẳng d đi qua M, cắt và vuông góc với Δ là:
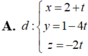
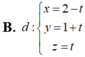
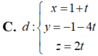
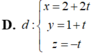
Trong không gian với hệ tọa độ Oxyz, cho các điểm M (2;2; -3) và N (-4; 2; 1). Gọi Δ là đường thẳng đi qua M, nhận vecto làm vectơ chỉ phương và song song với mặt phẳng (P): 2x+y+z0 sao cho khoảng cách từ N đến Δ đạt giá trị nhỏ nhất. Biết |a|, |b| là hai số nguyên tố cùng nhau. Khi đó |a| + |b| + |c| bằng: A. 15 B. 13 C. 16 D. 14
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các điểm M (2;2; -3) và N (-4; 2; 1). Gọi Δ là đường thẳng đi qua M, nhận vecto làm vectơ chỉ phương và song song với mặt phẳng (P): 2x+y+z=0 sao cho khoảng cách từ N đến Δ đạt giá trị nhỏ nhất. Biết |a|, |b| là hai số nguyên tố cùng nhau. Khi đó |a| + |b| + |c| bằng:
A. 15
B. 13
C. 16
D. 14
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
-
3
-
1
y
-
3
-
2
z
+
2
1
và
d...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 : x - 3 - 1 = y - 3 - 2 = z + 2 1 và d 2 : x - 5 - 3 = y + 1 2 = z - 2 1 và mặt phẳng (P) có phương trình x+2y+3z-5=0. Đường thẳng Δ vuông góc với (P) cắt d1 và d2 có phương trình là:
![]()
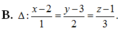
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
(
P
)
:
2
x
–
y
+
z
–
3
0
.
Phương trình chính tắc của của đường thẳng Δ đi qua điểm
M
(
-
2
;
1
;
1
)
và vuông góc với (P) l...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( P ) : 2 x – y + z – 3 = 0 . Phương trình chính tắc của của đường thẳng Δ đi qua điểm M ( - 2 ; 1 ; 1 ) và vuông góc với (P) là
A. x + 2 2 = y - 1 - 1 = z - 1 1
B. x - 2 2 = y - 1 - 1 = z - 1 1
C. x + 2 2 = y - 1 1 = z - 1 1
D. x + 2 2 = y - 1 - 1 = z - 1 - 1
Trong không gian với hệ tọa độ Oxyz cho hai điểm
A
(
1
;
-
1
;
1
)
,
B
(
-
1
;
2
;
3
)
và đường thẳng
∆
:
x
+
1
-
2
y
-
2
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai điểm A ( 1 ; - 1 ; 1 ) , B ( - 1 ; 2 ; 3 ) và đường thẳng ∆ : x + 1 - 2 = y - 2 1 = z - 3 3 . Phương trình đường thẳng d đi qua điểm A, đồng thời vuông góc với hai đường thẳng AB và Δ là
A. x - 7 1 = y - 2 - 1 = z - 4 1
B. x - 1 7 = y + 1 2 = z - 1 4
C. x + 1 7 = y - 1 - 2 = z + 1 4
D. x + 1 7 = y - 1 2 = z + 1 4
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng
d
:
x
-
3
1
y
-
3
3
z
2
, mặt phẳng (α): x+y-z+30 và điểm A (1;2;-1). Viết phương trình đường thẳng Δ đi qua A cắt d và song song với mặt phẳng (α).
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d : x - 3 1 = y - 3 3 = z 2 , mặt phẳng (α): x+y-z+3=0 và điểm A (1;2;-1). Viết phương trình đường thẳng Δ đi qua A cắt d và song song với mặt phẳng (α).
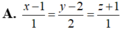
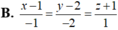
![]()
![]()




