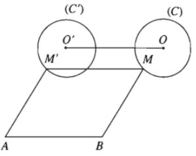
Do tứ giác ABMM’ là hình bình hành nên B A → = M M ' → là. Từ đó suy ra M' là ảnh của M qua phép tịnh tiến theo vectơ B A → .Từ đó suy ra tập hợp các điểm M' là đường tròn (C') , ảnh của C qua phép tịnh tiến theo vectơ BA→.
Cho hai điểm A, B và đường tròn tâm O không có điểm chung với đường thẳng AB. Qua mỗi điểm M chạy trên đường tròn (O) dựng hình bình hành MABN. Chứng minh rằng điểm N thuộc một đường tròn xác định.
Cho tứ diện ABCD. Qua điểm M nằm trên AC ta dựng một mặt phẳng (α) song song với AB và CD. Mặt phẳng này lần lượt cắt các cạnh BC, BD và AD tại N, P và Q.
a) Tứ giác MNPQ là hình gì?
b) Gọi O là giao điểm hai đường chéo của tứ giác MNPQ. Tìm tập hợp các điểm O khi M di động trên đoạn AC.
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính R và chiều cao là R 2 . Trên hai đường tròn (O) và (O') lần lượt lấy hai điểm A và B sao cho góc của hai đường thẳng OA và OB bằng α không đổi. Tính AB theo R và α .
A . R 1 + 4 sin 2 α 2
B . R + 4 sin 2 α 2
C . R 2 + 4 sin 2 α
D . R 1 + 4 sin 2 α
Cho đường tròn (C) và hai điểm cố định phân biệt A, B thuộc (C). Với mỗi điểm M chạy trên đường tròn (trừ hai điểm A, B), ta xét điểm N sao cho ABMN là hình bình hành. Chứng minh rằng tập hợp các điểm N cũng nằm trên một đường tròn xác định.
Cho hai tia Ax, By chéo nhau. Lấy M, N lần lượt là các điểm di động trên Ax, By. Gọi (α) là mặt phẳng chứa By và song song với Ax. Đường thẳng qua M và song song với AB cắt (α) tại M’.
a) Tìm tập hợp điểm M’.
b) Gọi I là trung điểm của MN. Tìm tập hợp các điểm I khi AM = BN
1. Cho hai đường trong (C1) và (C2) lần lượt có tâm O1, O2 và đều có bán kính R. Chứng minh rằng (C2) là ảnh của đường tròn (C1) qua phép đối xứng trục d, với d là đường trung trực của O1O2.
2. Cho hai điểm A và B nằm cùng phía của đường thẳng d. Hãy dựng điểm M trên d sao cho AM + BM bé nhất.
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. M là một điểm di động trên đoạn AB. Một mặt phẳng (α) đi qua M và song song với SA và BC; (α) cắt SB, SC và CD lần lượt tại N, P và Q
a) Tứ giác MNPQ là hình gì?
b) Gọi I là giao điểm của MN và PQ. Chứng minh rằng I nằm trên một đường thẳng cố định.
Cho 2 điểm phân biệt B,C cố định ( BC không phải là đường kính) trên đường tròn (O), điểm A di động trên (O), M là trung điểm BC, H là trực tâm tam giác ABC. Khi A di chuyển trên đường tròn (O) thì H di chuyển trên đường tròn (O;) là ảnh của (O) qua phép tịnh tiến theo u → . Khi đó bằng
A. B C →
B. O B →
C. 2 O M →
D. 2 O C →
Cho đường tròn (O,5) và a là điểm cố định trên đường tròn Gọi B C D là hai điểm di động trên đường tròn sao cho đoạn BC có độ dài không đổi bằng 8. gọi M là trung điểm của BC và G là trọng tâm tam giác ABC. khi B,C thay đổi trên đường tròn (O,5) thì tập hợp các điểm G là:
A. đường tròn có bán kính bằng 3
B. đường tròn có bán kính bằng 2
C. đường tròn có bán kính bằng 4
D. đường tròn có bán kính bằng 5
em đang cần gấp. cảm ơn ạ
