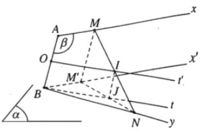
a) Gọi (β) là mặt phẳng xác định bởi hai đường thẳng AB và Ax
Do Ax // (α) nên (β) sẽ cắt (α) theo giao tuyến Bx’ song song với Ax.
Ta có M’ là điểm chung của (α) và (β) nên M’ thuộc Bx’.
Khi M trùng A thì M’ trùng B nên tập hợp M’ là tia Bx’.
Ta có tứ giác ABM’M là hình bình hành nên BM’ = AM = BN.
Tam giác BM’N cân tại B.
Suy ra trung điểm I của cạnh đáy NM’ thuộc phân giác trong Bt của góc B trong tam giác cân BNM’. Dễ thấy rằng Bt cố định.
Gọi O là trung điểm của AB. Trong mặt phẳng (AB, Bt), tứ giác OBIJ là hình bình hành nên I J → = B O → . Do đó I là ảnh của J trong phép tịnh tiến theo vectơ B O → . Vậy tập hợp I là tia Ot’ song song với Bt.



