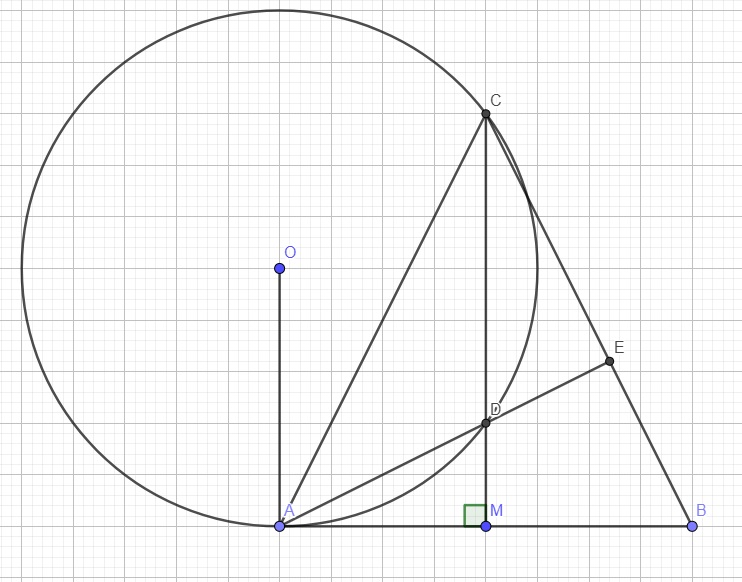
a.
Xét hai tam giác AMD và CMA có:
\(\left\{{}\begin{matrix}\widehat{AMD}=\widehat{CMA}=90^0\\\widehat{MAD}=\widehat{MCA}\left(\text{cùng chắn AD}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AMD\sim\Delta CMA\left(g.g\right)\)
\(\Rightarrow\dfrac{MA}{MC}=\dfrac{MD}{MA}\Rightarrow MA^2=MC.MD\)
Do A, M cố định \(\Rightarrow MA^2\) không đổi
\(\Rightarrow MC.MD\) không đổi
b.
Kéo dài AD cắt BC tại E
Từ cm câu a, \(\Delta AMD\sim\Delta CMA\Rightarrow\widehat{ADM}=\widehat{CAM}\)
Tam giác ADM vuông tại M \(\Rightarrow\widehat{ADM}+\widehat{MAD}=90^0\)
\(\Rightarrow\widehat{CAM}+\widehat{MAD}=90^0\) (1)
Mx đi qua trung điểm của AB và vuông góc AB nên Mx là trung trực của AB
C thuộc Mx \(\Rightarrow CA=CB\Rightarrow\Delta CAB\) cân tại C
\(\Rightarrow\widehat{CAM}=\widehat{CBM}\) (2)
(1);(2) \(\Rightarrow\widehat{MAD}+\widehat{CBM}=90^0\)
\(\Rightarrow\widehat{AEB}=180^0-\left(\widehat{MAD}+\widehat{CBM}\right)=90^0\)
\(\Rightarrow AE\perp BC\)
\(\Rightarrow D\) là giao điểm 2 đường cao AE và CM của tam giác ABC nên D là trực tâm tam giác ABC