b: Gọi O là điểm nằm trên đường trung trực của AB
=>OH⊥AB tại H
=>H là trung điểm của AB
Xét ΔOHA vuông tại H và ΔOHB vuông tại H có
OH chung
HA=HB
Do đó: ΔOHA=ΔOHB
Suy ra: OA=OB
Gọi M là một điểm cách đều hai đầu mút của đoạn thẳng AB. Chứng minh M nằm trên đường trung trực của AB.
a/ Cho hình vẽ . Phát biểu định lí dựa vào hình vẽ. Viết GT và KL của định lí đó.
b/
Vẽ hình theo diễn đạt bằng lời sau:
- Vẽ ΔABC .
- Vẽ đường thẳng d đi qua điểm A và song song với BC.
- Vẽ đường thẳng a là đường trung trực của BC
- Hỏi không? Vì sao?
Cho đoạn thẳng AB.Đường trung trực của đoạn thẳng AB cắt AB tại I. Lấy điểm M bất kì nằm trên đường trung trực của đoạn thẳng AB.
a/ Chứng minh: AM=MB.
b/ Chứng minh: MI là tia phân giác của góc AMB.
c/ Biết : Góc AMB bằng \(^{ }\)\(110^o\) . Hãy tính số đo góc ngoài tại đỉnh A.
Chứng minh đường thẳng PQ được vẽ như trong hình 43 đúng là đường trung trực của đoạn thẳng MN.
Gợi ý: Sử dụng định lí 2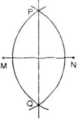
Hình 43
Trong các khẳng định sau, khẳng định sai là
A. Điểm cách đều 2 mút của 1 đoạn thẳng thì thuộc đường trung trực của đoạn thẳng đó
B. Qua 1 điểm nằm ngoài 1 đường thẳng chỉ có 1 đường thẳng song song với đường thẳng đó
C. Hai tam giác vuông có chung cạnh huyền thì bằng nhau
Trong các khẳng định sau, khẳng định sai là
A. Điểm cách đều 2 mút của 1 đoạn thẳng thì thuộc đường trung trực của đoạn thẳng đó
B. Qua 1 điểm nằm ngoài 1 đường thẳng chỉ có 1 đường thẳng song song với đường thẳng đó
C. Hai tam giác vuông có chung cạnh huyền thì bằng nhau
Trong các khẳng định sau, khẳng định sai là
A. Điểm cách đều 2 mút của 1 đoạn thẳng thì thuộc đường trung trực của đoạn thẳng đó
B. Qua 1 điểm nằm ngoài 1 đường thẳng chỉ có 1 đường thẳng song song với đường thẳng đó
C. Hai tam giác vuông có chung cạnh huyền thì bằng nhau
Cho đoạn thẳng BC cố định, M là trung điểm của đoạn thẳng BC. Vẽ góc CBx sao cho góc CBx = 45o, trên tia Bx lấy điểm A sao cho độ dài đoạn thẳng BM và BA tỉ lệ với 1 và √2. Lấy điểm D bất kì thuộc đoạn thẳng BM. Gọi H và I lần lượt là hình chiếu của B và C trên đường thẳng AD. Đường thẳng AM cắt CI tại N. Chứng minh rằng: a) DN vuông góc với AC. b) BH^2 + CI^ 2 có giá trị không đổi khi D di chuyển trên đoạn thẳng BM. c) Tia phân giác của góc HIC luôn đi qua một điểm cố định.
Vẽ hai đường thẳng aa' và bb' vuông góc với nhau tại M, trên đường thẳng aa' lấy hai điểm A, B sao cho M là trung điểm của AB. Trên đường thẳng bb' lấy hai điểm C, D sao cho CM=MD. Ghi đầy đủ kí hiệu lên hình vẽ và chứng tỏ đường thẳng bb' là đường trung trực của đoạn thẳng AB và đường thẳng aa' là đường trung trực của đoạn thẳng CD.
