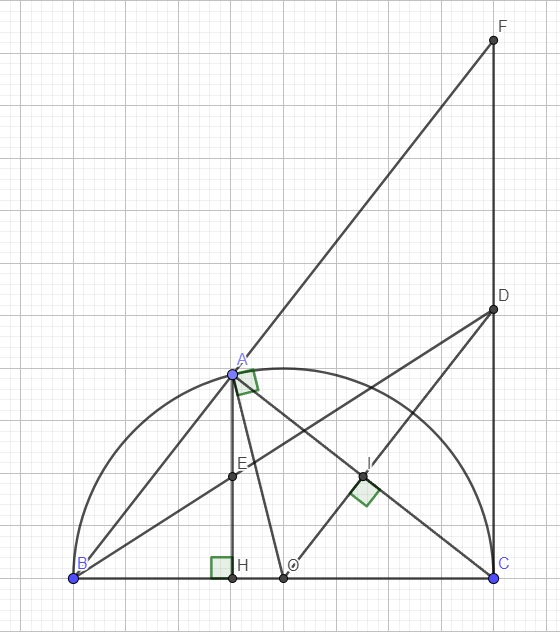
Cho điểm A thuộc nửa đường tròn tâm O có đường kính BC sao cho: AB < AC (A khác B). Gọi H là hình chiếu của A trên BC và I là trung điểm của AC.Tiếp tuyến tại A của nửa đường tròn (O) cắt BC ở S.
a) chứng minh tứ giác AHOI nội tiếp và AIH=2SAB
b) chứng minh SB.SC=SH.SO
c)chứng minh BH/BS=CH/CS
d) gọi D là giao điểm của SA và OI.chứng minh BD đi qua trung điểm của AH
Giúp mình câu d với
d.
Gọi E là giao điểm của AH và BD, kéo dài AB và CD cắt nhau tại F
Do I là trung điểm AC \(\Rightarrow OI\) là trung trực của AC
Mà D thuộc OI \(\Rightarrow DA=DC\Rightarrow\Delta DAO=\Delta DCO\left(c.c.c\right)\)
\(\Rightarrow\widehat{DAO}=\widehat{DCO}=90^0\)
\(\Rightarrow DC||AH\) (cùng vuông góc BC)
Trong tam giác BCF, ta có O là trung điểm BC và \(OD||BF\) (cùng vuông góc AC)
\(\Rightarrow OD\) là đường trung bình tam giác BCF
\(\Rightarrow D\) là trung điểm AF hay \(DC=DF\)
Do AH song song DC, áp dụng định lý Thales:
\(\left\{{}\begin{matrix}\dfrac{EH}{DC}=\dfrac{BE}{BD}\\\dfrac{EA}{DF}=\dfrac{BE}{BD}\end{matrix}\right.\) \(\Rightarrow\dfrac{EH}{DC}=\dfrac{EA}{DF}\)
\(\Rightarrow EH=EA\) \(\Rightarrow E\) là trung điểm AH hay BD đi qua trung điểm của AH