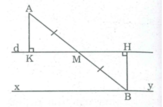
Kẻ AK ⊥ d,BH ⊥ d
Vì M thay đổi trên d, B đối xứng với A qua M nên AM = MB
Xét tam giác vuông AKM và BHM. Ta có: ∠ (AKM ) = ∠ (BHM ) = 90 0
AM = MB ( chứng minh trên)
∠ (AMK ) = ∠ (BMH ) ( đối đỉnh)
Do đó ∆ AKM = ∆ BHM ( cạnh huyền,góc nhọn) ⇒ AK = BH
Điểm A cố định, đường thẳng d cố định nên AK không đổi.
M thay đổi, B thay đổi cách đường thẳng d cố định một khoảng bằng AK không thay đổi nên B chuyển động trên đường thẳng xy song song với d và cách d một khoảng bằng AK.










