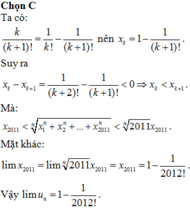Các câu hỏi tương tự
1) biết các nghiệm của phương trình \(cos2x=-\dfrac{1}{2}\) có dạng \(x=\dfrac{\pi}{m}+k\pi,k\in Z\) với m,n là các số nguyên dương. Khi đó m+n bằng
2) cho \(x=\dfrac{\pi}{3}+k2\pi\left(k\in Z\right)\) là nghiệm của phương trình
3) cho \(x=\dfrac{\pi}{2}+k\pi\left(k\in Z\right)\) là nghiệm của phương trình
Cho dãy (
X
k
) được xác định như sau
x
k
1
2
!
+
2
3
!
+
.
.
.
+
k
(
k
+
1
)
!
. Tìm l...
Đọc tiếp
Cho dãy ( X k ) được xác định như sau x k = 1 2 ! + 2 3 ! + . . . + k ( k + 1 ) ! . Tìm lim u n với u n = x 1 n + x 2 n + . . . + x 2017 n n
A. + ∞
B. - ∞
C. 1 - 1 2017 !
D. 1 + 1 2017 !
Cho dãy số được xác định bởi: U1=12
\(\frac{2\cdot U_{n+1}}{n^2+5n+6}=\frac{U_n+n^2-n-2}{n^2+n}\)
Tìm số hạng tổng quát của dãy số
tìm tất cả các bộ (n,k,p), với n,k là các số nguyên lớn hơn 1 và p là 1 số nguyên tố thỏa mãn \(n^5+n^4-2n^3-2n^2+1=p^k\)
Trong không gian, cho bốn mặt cầu có bán kính lần lượt là 2, 3, 3, 2 (đơn vị độ dài) tiếp xúc ngoài với nhau. Mặt cầu nhỏ nhất tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng?
Cho Sleft{1,2,...,nright}, A_isubset S, ioverline{1,k} thỏa mãn các điều kiện sau:
i) left|A_iright|gedfrac{n}{2},forall ioverline{1,k}
ii) left|A_icap A_jright|ledfrac{n}{4},forall ine j;i,joverline{1,k}
Chứng minh rằng left|A_1cup A_2cup...cup A_kright|gedfrac{kn}{k+1}
Đọc tiếp
Cho \(S=\left\{1,2,...,n\right\}\), \(A_i\subset S\), \(i=\overline{1,k}\) thỏa mãn các điều kiện sau:
i) \(\left|A_i\right|\ge\dfrac{n}{2},\forall i=\overline{1,k}\)
ii) \(\left|A_i\cap A_j\right|\le\dfrac{n}{4},\forall i\ne j;i,j=\overline{1,k}\)
Chứng minh rằng \(\left|A_1\cup A_2\cup...\cup A_k\right|\ge\dfrac{kn}{k+1}\)
Cho dãy số
u
(
n
)
xác định bởi
u
(
1
)
1
;
u
(
m
+
n
)
u...
Đọc tiếp
Cho dãy số u ( n ) xác định bởi u ( 1 ) = 1 ; u ( m + n ) = u ( m ) + u ( n ) + m n , ∀ m , n ∈ ℕ * . Tính u ( 2017 )
A. 2035153
B. 2035154
C. 2035155
D. 2035156
Trong mặt phẳng Oxy, cho điểm M(4;3) và đường tròn (C)\(\left(x-1\right)^2+\left(y+1\right)^2=16\) .Viết phương trình đường tròn (C') là ảnh của C qua phép vị tự tâm I(1;-1) tỉ số k. Xác định tỉ số k sao cho (C') đi qua M
tìm tất cả các bộ (n,k,p), với n,k là các số nguyên lớn hơn 1 và p là 1 số nguyên tố thỏa mãn \(n^5+n^4-2n^3-2n^2+1=p^k\)