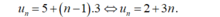
Chọn B.
- Ta có, u 1 = 5 và u n + 1 = 3 + u n nên dãy số là cấp số cộng với công sai d = 3, số hạng đầu u 1 = 5 .
- Do đó số hạng tổng quát của dãy số này là:
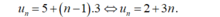
Cho dãy số (Un) xác định bởi U1=-3 và U(n+1)=Un+ n^2 -3n +4, mọi n thuộc N*. Số 1391 là số hạng thứ mấy của dãy ?
Cho dãy số được xác định bởi: U1=12
\(\frac{2\cdot U_{n+1}}{n^2+5n+6}=\frac{U_n+n^2-n-2}{n^2+n}\)
Tìm số hạng tổng quát của dãy số
Cho dãy số u ( n ) xác định bởi u ( 1 ) = 1 ; u ( m + n ) = u ( m ) + u ( n ) + m n , ∀ m , n ∈ ℕ * . Tính u ( 2017 )
A. 2035153
B. 2035154
C. 2035155
D. 2035156
Cho dãy số xác định bởi u1=1 , u n+1 = \(2un+\frac{n-1}{n^2+3n+2}\). khi đó u 2018 bằng
Cho dãy số u(n)=\(1/(2*4) +1/(5*7)+...+1/((3n-1)*(3n+1))\)
Tính Lim u(n).
Cho dãy số u n xác định bởi u 1 = 321 và u n + 1 = u n - 3 với mọi n ∈ N * . Tính tổng S của 125 số hạng đầu tiên của dãy số đó.
A. S = 16875
B. S = 63375
C. S = 63562,5
D. S = 16687,5
Cho dãy số \(\left(a_n\right)\) xác định bởi công thức:
\(\hept{\begin{cases}a_1=1;a_2=2;\\na_{n+2}=\left(3n+2\right)a_{n+1}-2\left(n+1\right)a_n;n=1;2;3...\end{cases}}\)
a) Tìm công thức số hạng tổng quát của dãy \(\left(a_n\right)\)
b)Chứng minh \(\sqrt{a_1-1}+\sqrt{a_2-1}+...+\sqrt{a_n-1}\ge\frac{n\left(n+1\right)}{2};\forall n\inℕ^∗\)
c) Tính \(lim\left(\frac{a_1}{3}+\frac{a_2}{3^2}+...+\frac{a_n}{3^n}\right)\)
1) cho dãy số được xác định bởi
a) Tính
2) cho dãy số được xác định bởi
b) \(\dfrac{13}{7}\) là số hạng thứ mấy của dãy
