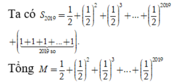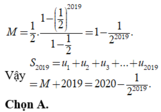
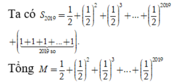là tổng 2019 số hạng đầu tiên của một cấp số nhân với số hạng đầu
u
1
=
1
2
, công bội q=
1
2
Do đó
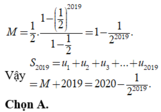
Cho dãy số u n xác định bởi u 1 = 1 u n + 1 = u n 2 + 2 u n + 2019 , n ≥ 2 , n ∈ ℕ Tính l i m u n + 1 u n
A. 1
B. + ∞
C. 2018
D . 2017 2018
Cho dãy số u n xác định bởi u 1 = 0 và u n + 1 = u n + 4 n + 3 với ∀ n ≥ 2 . Biết rằng dãy số thỏa mãn l i m u n + u 4 n + u 4 2 n + . . . + u 4 2018 n u n + u 2 n + u 2 2 n + . . . + u 2 2018 n = a 2019 + b c với a, b, c là các số nguyên dương và b < 2019. Tính giá trị của S = a + b - c
A. S = -1
B. S = 0
C. S = 2017
D. S = 2018
Cho hàm số f x = ln 2019 - ln x + 1 x . Tổng f ' 1 + f ' 2 + f ' 3 + . . . + f ' 2019 bằng
A. 2019
B. 2018 2019
C. 2018
D. 2019 2020
Xét các khẳng định sau
i) Nếu a > 2019 thì a x > 2019 x ∀ x ∈ ℝ
ii) Nếu a > 2019 thì b a > b 2019 ∀ b > 0
iii) Nếu a > 2019 thì log b a > log b 2019 ∀ n > 0 ; b ≢ 0
Số khẳng định đúng trong các khẳng định trên là:
A. 3
B. 1
C. 2
D. 0
Cho hàm số f(x) = ( x - 1 )( x - 2 )( x - 3 )...( x - 2019 ). Tính f '(1)
A. 0
B. 1
C. 2018!
D. 2019!
Số giá trị nguyên của tham số m nằm trong khoảng (0.2020) để phương trình x - 1 - 2019 - x = 2020 - m có nghiệm là
A. 2020
B. 2021
C. 2019
D. 2018
Tìm số nguyên dương n sao cho
C 2 n + 1 1 - 2 . 2 . C 2 n + 1 2 + 3 . 2 . C 2 n + 1 3 - 4 . 2 3 . C 2 n + 1 4 + . . + 2 n + 1 2 2 n C 2 n + 1 2 n + 1 = 2019
A. 1009
B. 1010
C. 1011
D. 1012
Cho hàm số y=f(x)=x(x+1)(x+2)(x+3)...(x+2018)(x+2019). Tínhf’(0).
A. 0.
B. 2019 1 + 2019 2
C. P 2019
D. 2019
Trong 2019 điểm phân biệt cho trước, có bao nhiêu vectơ khác 0 → với điểm đầu và điểm cuối là 2 trong 2019 điểm đã cho?
A. C 2019 2
B. 2019 2
C. A 2019 2017
D. A 2019 2
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d thỏa mãn a,b,c,dÎR; a > 0 và d > 2019 8 a + 4 b + 2 x + d - 2019 < 0 . Số cực trị của hàm số y = | f ( x ) - 2019 | bằng
A. 3
B. 2
C. 1
D. 5
