Ta có:
0 = 0 0 + 1 ; 1 2 = 1 1 + 1 ; 2 3 = 2 2 + 1 3 4 = 3 3 + 1 ; 4 5 = 4 4 + 1
Suy ra u n = n n + 1
Chọn đáp án B
Ta có:
0 = 0 0 + 1 ; 1 2 = 1 1 + 1 ; 2 3 = 2 2 + 1 3 4 = 3 3 + 1 ; 4 5 = 4 4 + 1
Suy ra u n = n n + 1
Chọn đáp án B
Cho dãy số có các số hạng đầu là : 5,10,15,20,25,..số hạng tổng quát của dãy số trên là : A.Un=5(n-1) B.Un=5n C.Un=5+n D.Un=5n+1
Cho dãy số (Un) xác định bởi U1=-3 và U(n+1)=Un+ n^2 -3n +4, mọi n thuộc N*. Số 1391 là số hạng thứ mấy của dãy ?
Cho dãy số được xác định bởi: U1=12
\(\frac{2\cdot U_{n+1}}{n^2+5n+6}=\frac{U_n+n^2-n-2}{n^2+n}\)
Tìm số hạng tổng quát của dãy số
6) cho dãy số có các số hạng đầu tiên là 8,15,22,29,36,.. số hạng tổng quát của dãy số là
7) cho dãy số \(\left(u_n\right)\) với \(u_n=\dfrac{2n+5}{5n-4}\) với mọi n ϵ N* cho biết số hạng thứ n là \(\dfrac{7}{12}\), giá trị của n là
8) cho dãy số \(\left(u_n\right)\) với \(u_n=\dfrac{2n}{n^2+1}\) với mọi n ϵ N* số \(\dfrac{9}{41}\) là số hạng thứ bao nhiêu trong dãy số
9) trong các dãy số \(\left(u_n\right)\) cho bởi số hạng tổng quát \(u_n\) sau, dãy số nào là dãy số tăng
A.\(u_n=\left(\dfrac{2}{3}\right)^n\)
B. \(u_n=\dfrac{n}{n+1}\)
C. \(u_n=\dfrac{2}{n.\left(n+1\right)}\)
D. \(u_n=\dfrac{n+1}{n}\)
10) trong các dãy số \(\left(u_n\right)\) cho bởi số hạng tổng quát \(u_n\) sau, dãy số nào là dãy số giảmA. \(u_n=3^n\)B. \(u_n=\dfrac{n-3}{n+1}\)C. \(u_n=\dfrac{n+4}{n+2}\)D. \(u_n=n^4+2\)Cho dãy số \(\left(a_n\right)\) xác định bởi công thức:
\(\hept{\begin{cases}a_1=1;a_2=2;\\na_{n+2}=\left(3n+2\right)a_{n+1}-2\left(n+1\right)a_n;n=1;2;3...\end{cases}}\)
a) Tìm công thức số hạng tổng quát của dãy \(\left(a_n\right)\)
b)Chứng minh \(\sqrt{a_1-1}+\sqrt{a_2-1}+...+\sqrt{a_n-1}\ge\frac{n\left(n+1\right)}{2};\forall n\inℕ^∗\)
c) Tính \(lim\left(\frac{a_1}{3}+\frac{a_2}{3^2}+...+\frac{a_n}{3^n}\right)\)
Cho dãy số (un) được xác định như sau: u 1 = 1 u n = 3 u n - 1 + 1 2 u n - 1 - 2 , n ≥ 2 Viết 4 số hạng đầu của dãy và chứng minh rằng un > 0, ∀ n
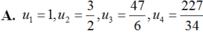
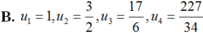
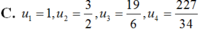
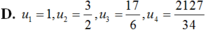
Dãy số u n cho bởi u 1 = 3 , u n + 1 = 1 + u n 2 , n > 1
a. Viết năm số hạng đầu của dãy số.
b. Dự đoán công thức số hạng tổng quát un và chứng minh công thức đó bằng phương pháp quy nạp.