Trong ΔABC, ta có: AD là đường phân giác của (BAC)
Suy ra: 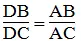 (tính chất đường phân giác)
(tính chất đường phân giác)
Mà AB = 21 (cm); AC = 28 (cm)
Nên \(\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{21}{28}=\dfrac{3}{4}\)
Suy ra:
(tính chất tỉ lệ thức)Suy ra:
Hình vẽ
a) Diện tích \(\Delta ABC\) : \(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.21.28=294\left(cm^2\right)\)
Do AH là đường cao ( gt ) \(\Rightarrow\widehat{AHB}=\widehat{AHC}=90^o\)
Xét \(\Delta ABC\) và \(\Delta HAC\) có : \(\left\{{}\begin{matrix}\widehat{BAC}=\widehat{AHC\left(=90^o\right)}\\\widehat{HCA}chung\end{matrix}\right.\)
\(\Rightarrow\Delta ABC\sim\Delta HAC\left(g.g\right)\)
\(\Rightarrow\dfrac{AH}{AB}=\dfrac{AC}{BC}\)
\(\Rightarrow AH.BC=AB.AC\left(đpcm\right)\)
b) Trong \(\Delta ABC\) vuông tại A ( gt)
\(\Rightarrow BC^2=AB^2+AC^2\left(Pytago\right)\)
\(\Leftrightarrow BC^2=21^2+28^2\)
\(\Leftrightarrow BC^2=441+784\)
\(\Leftrightarrow BC^2=1225\)
\(\Rightarrow BC=35\left(cm;BC>0\right)\)




 hình vẽ
hình vẽ câu a)
câu a)







