Tổng số cạnh và đường chéo của đa giác n cạnh là n(n-1)/2, suy ra số đường chéo của đa giác là
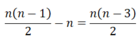
Vì mỗi đường chéo xác định hai vectơ, nên tổng số vectơ là n(n – 3)
Đáp án D
Tổng số cạnh và đường chéo của đa giác n cạnh là n(n-1)/2, suy ra số đường chéo của đa giác là
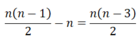
Vì mỗi đường chéo xác định hai vectơ, nên tổng số vectơ là n(n – 3)
Đáp án D
Cho một đa giác đều 24 đỉnh. Hỏi: 1. Đa giác có bao nhiêu đường chéo? 2. Từ các đỉnh của đa giác, lập được bao nhiêu: a. Đoạn thẳng. b. Vectơ khác vectơ-không. c. Tam giác.
Câu 8: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của AD và BC, có bao nhiêu vectơ bằng với DM từ các điểm đã cho? A. 3. B. 4. C. 5. D. Câu 9: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chọn khẳng định đúng trong các khẳng định sau.
A. AD BC . B. MQ PN . C. MN QP . D. AB DC .
Câu 10: Cho tam giác ABC với trực tâm H, D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây là đúng
A. HA CD và AD CH .
B. HA CD và DA HC .
C. HA CD và AD HC .
D. HA CD và AD HC và OB OD .
Câu 1: Cho ABCD là hình vuông cạnh bằng 1. Khi đó độ dài của AC bằng
A. 1. B. 2. C. 2. D. 3.
Câu 2: Cho tam giác ABC vuông tại C có cạnh AC cm BC cm 4 , 3 . Độ dài của vectơ AB là
A. 7 . cm B. 6 . cm C. 5 . cm D. 4 . cm
Câu 3: Cho hình vuông ABCD tâm O, cạnh 2a. Độ dài vectơ DO bằng
A. 2 2. a B. 2 . 2 a C. a 2. D. 2 2. a
Câu 4: Cho đoạn thẳng AB cm 10 , điểm C thỏa mãn AC CB . Độ dài vectơ AC là
A. 10 . cm B. 5 . cm C. 20 . cm D. 15 . c
Cho tam giác ABC, trên cạnh BC lấy điểm D sao cho BD= 2/3 BC, M là trung điểm của đoạn thẳng AD, điểm N thoả mãn điều kiện vectơ AN = 2/5 vectơ AC. Chứng minh 3 điểm B , M ,N thẳng hàng.
Trong mặt phẳng Oxy, cho điểm A(2;-4), đường thẳng Δ: x = -3 + 2t, y = 1 + t và đường tròn (C): x^2 + y^2 – 2x – 8y – 8 = 0.
a. Tìm một vectơ pháp tuyến n của đường thẳng Δ. Lập phương trình tổng quát của đường thẳng d, biết d đi qua điểm A và nhận n làm vectơ pháp tuyến.
b. Viết phương trình đường tròn (T), biết (T) có tâm A và tiếp xúc với Δ.
c. Gọi P, Q là các giao điểm của Δ và (C). Tìm toạ độ điểm M thuộc (C) sao cho tam giác MPQ cân tại M.
Cho một đa giác đều 24 đỉnh. Hỏi a.Đa giác có bao nhiêu đường chéo. Từ các đỉnh của đa giác lập được bao nhiêu: b,Tam giác vuông c,Tam giác đều d,Tứ giác e,Hình chữ nhật mà không phải là hình vuông
Cho một đa giác đều 24 đỉnh. Hỏi a.Đa giác có bao nhiêu đường chéo. Từ các đỉnh của đa giác lập được bao nhiêu: b,Tam giác vuông c,Tam giác đều d,Tứ giác e,Hình chữ nhật mà không phải là hình vuông
Cho một đa giác đều 24 đỉnh. Hỏi a.Đa giác có bao nhiêu đường chéo. Từ các đỉnh của đa giác lập được bao nhiêu: b,Tam giác vuông c,Tam giác đều d,Tứ giác e,Hình chữ nhật mà không phải là hình vuông
Cho một đa giác đều 24 đỉnh. Hỏi a.Đa giác có bao nhiêu đường chéo. Từ các đỉnh của đa giác lập được bao nhiêu: b,Tam giác vuông c,Tam giác đều d,Tứ giác e,Hình chữ nhật mà không phải là hình vuông