Chọn C.
Phương pháp:
Số đường chéo của đa giác có n đỉnh
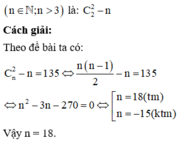
Chọn C.
Phương pháp:
Số đường chéo của đa giác có n đỉnh
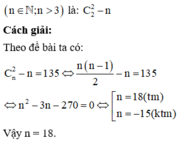
Cho đa giác đều n đỉnh, n ∈ N v à n ≥ 3 . Tìm n biết rằng đa giác đã cho có 135 đường chéo
A. n = 15
B. n = 27
C. n = 8
D. n = 18
Cho một đa giác đều n đỉnh, nÎN, n≥3. Tìm n biết rằng đa giác đã cho có 27 đường chéo.
A. 12
B. 10
C. 9
D. 16
Cho đa giác đều n cạnh ( n ≥ 4 ) . Tìm n để đa giác có số đường chéo bằng số cạnh?
A. n = 5
B. n = 16
C. n = 6
D. n = 8
Cho đa giác đều A 1 A 2 . .. A 2 n n ≥ 2 , n ∈ Z nội tiếp đường tròn O. Biết rằng số tam giác trong 2n điểm A 1 , A 2 , . .. , A 2 n gấp 20 lần số hình chữ nhật có 4 đỉnh trong 2n điểm đó. Tìm n.
A. 12
B. 8
C. 16
D. 10
Cho một đa giác đều gồm 2n đỉnh (n≥2, nÎN*). Chọn ngẫu nhiên ba đỉnh trong sổ 2n đỉnh của đa giác, xác suất ba đỉnh được chọn tạo thành một tam giác vuông là 1 5 . Tìm n.
A. 5
B. 4
C. 10
D. 8
Cho (H) là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O ![]() . Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là
3
29
. Tìm n?
. Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là
3
29
. Tìm n?
A. 20
B. 12
C. 15
D. 10
Cho một đa giác đều gồm 2n đỉnh n ≥ 2 , n ∈ ℕ . Chọn ngẫu nhiên ba đỉnh trong số 2n đỉnh của đa giác, xác suất ba đỉnh được chọn tạo thành một tam giác vuông là 1/5. Tìm n .
A. 5
B. 4
C. 10
D. 8
Cho một đa giác đều 2n đỉnh 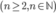 Tìm n biết số hình chữ nhật được tạo ra từ bốn đỉnh trong số 2n đỉnh của đa giác đó là 45
Tìm n biết số hình chữ nhật được tạo ra từ bốn đỉnh trong số 2n đỉnh của đa giác đó là 45
A. n = 12
B. n = 10
C. n = 9
D. n = 45
Cho đa giác đều 2n đỉnh n ≥ 2 . Hỏi có bao nhiêu hình chữ nhật có 4 đỉnh là 4 trong 2n đỉnh của đa giác.
A. C 2 n 2
B. C n 4
C. C 2 n 4
D. C n 2