Chọn D
Gọi tổng số các đỉnh của (H) là đ và tổng số các cạnh của (H) là c. Ta có 5đ = 2c. Do đó c > 10, đ > 4 và đ chia hết cho 2, c chia hết cho 5
Chọn D
Gọi tổng số các đỉnh của (H) là đ và tổng số các cạnh của (H) là c. Ta có 5đ = 2c. Do đó c > 10, đ > 4 và đ chia hết cho 2, c chia hết cho 5
Chứng minh rằng một đa diện mà mỗi đỉnh của nó đều là đỉnh chung của số lẻ mặt thì tổng số các đỉnh của nó là một số chẵn. Cho ví dụ.
Cho các phát biểu sau:
(1). Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
(2). Hai đa giác phân biệt của một hình đa diện chỉ có thể có thể hoặc không có điểm chung,
hoặc chỉ có một đỉnh chung, hoặc một cạnh chung.
(3). Mỗi cạnh của đa giác nào của một hình đa diện cũng là cạnh chung của đúng hai đa giác.
Số phát biểu đúng là
A. 0
B. 1
C. 3
D. 2
Cho khối đa diện (H) có các đỉnh là tâm các mặt bên của một hình lập phương có cạnh bằng 4. Xét hình nón tròn xoay (N) đi qua tất cả các đỉnh của đa diện (H), đỉnh và tâm đáy của (N) lần lượt là hai đỉnh của đa diện (H) nằm trên hai mặt bên đối lập nhau của hình lập phương (hình vẽ). Thể tích V của khối nón tròn xoay (N) bằng
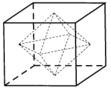
A. 256 π
B. 64 π
C. 64 π 3
D. 16 π 3
Cho một đa giác đều (H) có 15 đỉnh. Người ta lập một tứ giác có 4 đỉnh là 4 đỉnh của (H). Tính số tứ giác được lập thành mà không có cạnh nào là cạnh của (H).
A. 4950
B. 1800
C. 30
D. 450
Cho đa diện (H), biết rằng mỗi mặt của (H) đều là những đa giác có số cạnh là lẻ và tồn tại ít nhất một mặt có số cạnh khác với các mặt còn lại. Hỏi khẳng định nào đúng trong các khẳng định sau
A. Tổng số các cạnh của (H) bằng 9
B. Tổng số các cạnh của (H) bằng 5
C. Tổng số các cạnh của (H) là số lẻ
D. Tổng số các cạnh của (H) là số chẵn
Cho khối đa diện có mỗi đỉnh là đỉnh chung của đúng ba cạnh. Khi đó số đỉnh của khối đa diện là :
A. Số tự nhiên lớn hơn 3
B. Số lẻ
C. Số tự nhiên chia hết cho 3.
D. Số chẵn
Cho đa giác lồi (H) có 22 cạnh. Gọi X là tập hợp của các tam giác có 3 đỉnh là ba đỉnh của (H). Chọn ngẫu nhiên hai tam giác trong X. Tính xác suất để chọn được 1 tam giác có 1 cạnh là cạnh của đa giác (H) và 1 tam giác không có cạnh nào là cạnh của đa giác (H) (Kết quả làm tròn đến số thập phân thứ ba)
A. 0,374
B. ,0375
C. 0,376.
D. 0,377
Cho một đa diện có đỉnh và mỗi đỉnh là đỉnh chung của đúng 3 cạnh. Chọn mệnh đề đúng trong các mệnh đề sau
A. m là một số lẻ.
B. m chia hết cho 5.
C. m chia hết cho 3.
D. m là một số chẵn.
Cho đa giác đều (H) có 20 cạnh. Xét tam giác có 3 đỉnh được lấy từ các đỉnh của (H). Hỏi có bao nhiêu tam giác có đúng1 cạnh là cạnh của (H)
A. 320
B. 360
C. 380
D. 400