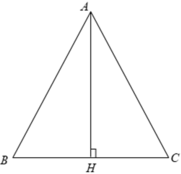
Xét Δ ABC cân tại A có BC = 30( cm )
⇒ BH = CH = 15( cm ).
Áp dụng đinh lý Py – ta – go ta có:
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Cho Δ ABC cân tại A có BC = 30( cm ), đường cao AH = 20 ( cm ). Tính đường cao ứng với cạnh bên của tam giác cân đó.
cho tam giác ABC cân tại A có BC = 6cm, đường cao AH = 4cm. tính đường cao ứng với cạnh bên
một tam giác cân có đường cao ứng với cạnh đáy bằng 15 cm, đường cao ứng với cạnh bên bằng 20 cm. Tính các cạnh của tam giác đó hoặc làm tròn đến chữ số thập phân thứ nhất.
4. a)Tính cạnh góc vuông của một tam giác vuông cân có cạnh huyền bằng a.
b) Tính cạnh của một tam giác đều có đường cao bằng h.
5. Cho tam giác nhọn ABC, đường cao AH = 12 cm, AB = 13 cm, HC = 16 cm. Tính các độ dài AC, BC.
Cho tam giác ABC cân tại A, BC = 15 cm, đường cao AH = 10 cm. Tính diện tích hình tam giác ABC , kẻ CK vuông với AB, tính CK
Tính độ dài cạnh BC của tam giác ABC cân tại A.Biết đường cao ứng với cạnh đáy bằng 15,6cm và đường cao ứng với cạnh bên bằng 12cm.
1/ Tính S hình thoi có cạnh 17cm , tổng 2 đường chéo 46cm2/ Cho hìh thag cân ABCD , AB // CD, AB CD. Kẻ đường cao AH. Biết AH 8cm, HC 12cm.Tíh S hìh thag ABCD3/ Cho tam giác can có đường cao ứng với cạh đáy 15cm., đường cao ứng với cạh bên 20 cm.Tíh các cạh của tam giác đó4/ Cho tam giác ABC, các đường trug tuyến BD, CE. Biết BC 10cm, BD 4cm, CE 12cm. a) C/m rằng BD vuông góc CE b) Tíh S tam giác ABC
Đọc tiếp
1/ Tính S hình thoi có cạnh = 17cm , tổng 2 đường chéo = 46cm
2/ Cho hìh thag cân ABCD , AB // CD, AB < CD. Kẻ đường cao AH. Biết AH = 8cm, HC = 12cm.Tíh S hìh thag ABCD
3/ Cho tam giác can có đường cao ứng với cạh đáy = 15cm., đường cao ứng với cạh bên = 20 cm.Tíh các cạh của tam giác đó
4/ Cho tam giác ABC, các đường trug tuyến BD, CE. Biết BC = 10cm, BD = 4cm, CE = 12cm.
a) C/m rằng BD vuông góc CE
b) Tíh S tam giác ABC
cho tam giác ABC vuông tại A. Đường cao AH chia cạnh BC ra làm 2 đoạn (CH = 9 cm, BH = 4 cm)
a) chứng minh tam giác HBA đồng dạng tam giác ABC
b) Tính AH, AB
c) trên HC, lấy điểm I sao cho AH=HI. Đường thẳng qua I vuông góc với cạnh BC cắt AC ở K. Chứng minh tam giác ABK cân.
Câu 1.Cho tam giác ABC có AB 24 cm, AC 30 cm. Trên cạnh AB và AC lần lượtlấy các điểm M và N sao cho AM 8 cm, AN 10 cm.1.Chứng minh MN//BC2. Tính MN biết BC 36 cmCâu 2. Cho tam giác ABC có AB 10 cm, AC 20 cm. Trên cạnh AC đặt đoạn thẳngAD 5 cm. Chứng minh ABD ACB [Câu 3. Cho tam giác ABC vuông tại A và phân giác AD (D ∈ BC). Biết AB 15 cm,AC 20 cm. Tính DB và DC.Câu 4.Cho tam giác ABC vuông tại A (AB AC) và đường cao AH.1. Chứng minh BA2 BH.BC.2. Tính độ dài cạnh AC khi biết AB 3...
Đọc tiếp
Câu 1.Cho tam giác ABC có AB = 24 cm, AC = 30 cm. Trên cạnh AB và AC lần lượt
lấy các điểm M và N sao cho AM = 8 cm, AN = 10 cm.
1.Chứng minh MN//BC
2. Tính MN biết BC = 36 cm
Câu 2. Cho tam giác ABC có AB = 10 cm, AC = 20 cm. Trên cạnh AC đặt đoạn thẳng
AD = 5 cm. Chứng minh ABD \= ACB [
Câu 3. Cho tam giác ABC vuông tại A và phân giác AD (D ∈ BC). Biết AB = 15 cm,
AC = 20 cm. Tính DB và DC.
Câu 4.Cho tam giác ABC vuông tại A (AB < AC) và đường cao AH.
1. Chứng minh BA2 = BH.BC.
2. Tính độ dài cạnh AC khi biết AB = 30 cm, AH = 24 cm.
3. Trên cạnh AC lấy điểm M sao cho CM = 10 cm, trên cạnh BC lấy điểm N sao cho CN
= 8 cm. Chứng minh tam giác CMN vuông.
4. Chứng minh CM.CA = CN.CB
Câu 5. (7đ) Cho tam giác ABC nhọn và đường cao AH. Kẻ HI ⊥ AB và HK ⊥ AC.
1. Chứng minh AH2 = AI.AB.
2. Chứng minh 4AIK v 4ACB
3. Đường phân giác của góc AHB cắt AB tại E. Biết EB/ AB = 2/ 5 . Tính tỉ số BI /AI
Câu 6. Cho tam giác AOB cân tại O (O <b 90◦
) và hai đường cao AD, BE. Đường vuông
góc với OA tại A cắt tia OB tại C. Chứng minh:
1. ED//AB.
2. OB2 = OE.OC
3. AB là đường phân giác của DAC \.
4. (Chứng minh BD.OA = BC.OE
giúp mình với nhé :( cần gấp